Question Number 159035 by HongKing last updated on 12/Nov/21

Commented by mr W last updated on 12/Nov/21

$${no}\:{unique}\:{solution}\:{possible}. \\ $$$${we}\:{can}\:{select}\:{a}\:{very}\:{small}\:{value}\:{for} \\ $$$${z}=\delta\:{with}\:\delta\rightarrow\mathrm{0}.\:{then}\:{we}\:{have} \\ $$$${m}={min}\left(×,\:×,\:×\right)\:\rightarrow\mathrm{0} \\ $$$${i}.{e}.\:{m}\:{doesn}'{t}\:{exist}! \\ $$$$ \\ $$$${i}\:{think}\:{the}\:{question}\:{should}\:{be} \\ $$$${m}={max}\left(×,×,×\right) \\ $$
Commented by HongKing last updated on 12/Nov/21

$$\mathrm{no}\:\mathrm{there}\:\mathrm{is}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{my}\:\mathrm{problem} \\ $$$$\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser} \\ $$
Commented by mr W last updated on 12/Nov/21

$${then}\:{please}\:{share}\:{your}\:{solution}: \\ $$$${how}\:{large}\:{is}\:{m}? \\ $$$${please}\:{don}'{t}\:{just}\:{say},\:{but}\:{also}\:{do}! \\ $$$${otherwise}\:{it}'{s}\:{not}\:{fair}\:{from}\:{you}, \\ $$$${because}\:{i}\:{always}\:{tell}\:{you}\:{my}\:{complete} \\ $$$${solution},\:{but}\:{you}\:{just}\:{say}\:{you}\:{have} \\ $$$${the}\:{solution}\:{without}\:{telling}\:{how}\:{the} \\ $$$${solution}\:{is}. \\ $$
Commented by HongKing last updated on 12/Nov/21

$$\mathrm{assume}\:\mathrm{that}\:\rightarrow\:\mathrm{m}\:\geqslant\:\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{have}\:\left(\mathrm{2ab}^{\mathrm{2}} +\mathrm{b}^{\mathrm{3}} \mathrm{c}\right)\left(\mathrm{2bc}^{\mathrm{2}} +\mathrm{c}^{\mathrm{3}} \mathrm{a}\right)\left(\mathrm{2ca}^{\mathrm{2}} +\mathrm{a}^{\mathrm{3}} \mathrm{b}\right)\geqslant\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{by}\:\rightarrow\:\mathrm{AM}\:-\:\mathrm{GM}\:\rightarrow\:\mathrm{we}\:\mathrm{have}: \\ $$$$\left(\mathrm{2ab}^{\mathrm{2}} +\mathrm{b}^{\mathrm{3}} \mathrm{c}\right)\left(\mathrm{2bc}^{\mathrm{2}} +\mathrm{c}^{\mathrm{3}} \mathrm{a}\right)\left(\mathrm{2ca}^{\mathrm{2}} +\mathrm{a}^{\mathrm{3}} \mathrm{b}\right) \\ $$$$=\:\left(\mathrm{abc}\right)^{\mathrm{2}} \left(\mathrm{2a}+\mathrm{bc}\right)\left(\mathrm{2b}+\mathrm{ca}\right)\left(\mathrm{2c}+\mathrm{ab}\right) \\ $$$$\overset{\boldsymbol{\mathrm{AM}}-\boldsymbol{\mathrm{GM}}} {\leqslant}\:\left(\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{3}}\right)^{\mathrm{6}} \left(\frac{\mathrm{2}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\leqslant\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{6}} \left(\frac{\mathrm{2}\centerdot\mathrm{2}}{\mathrm{3}}\:+\:\frac{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} }{\mathrm{3}\centerdot\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$=\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{6}} \left(\frac{\mathrm{16}}{\mathrm{9}}\right)^{\mathrm{3}} =\:\left(\frac{\mathrm{8}}{\mathrm{9}}\right)^{\mathrm{6}} <\:\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{have}\:\rightarrow\:\mathrm{m}\:<\:\mathrm{1} \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{equation}\:\rightarrow\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{2x}\:+\:\mathrm{m}\:=\:\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{root}\:\rightarrow\:-\mathrm{1}\:\pm\:\sqrt{\mathrm{1}\:-\:\mathrm{m}}\:\bullet \\ $$
Commented by mr W last updated on 12/Nov/21
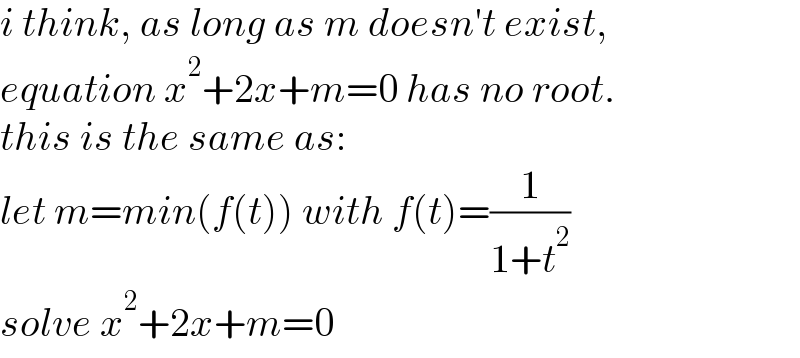
$${i}\:{think},\:{as}\:{long}\:{as}\:{m}\:{doesn}'{t}\:{exist},\: \\ $$$${equation}\:{x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0}\:{has}\:{no}\:{root}.\: \\ $$$${this}\:{is}\:{the}\:{same}\:{as}: \\ $$$${let}\:{m}={min}\left({f}\left({t}\right)\right)\:{with}\:{f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${solve}\:{x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0} \\ $$
Commented by HongKing last updated on 13/Nov/21

$$\mathrm{My}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{can}\:\mathrm{you}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{more} \\ $$$$\mathrm{about}\:\mathrm{this}\:\mathrm{fraction}\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:?\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand} \\ $$
Commented by mr W last updated on 13/Nov/21

$${i}\:{just}\:{want}\:{to}\:{say}:\:{the}\:{function}\: \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{is}\:{always}\:{less}\:{than}\:{or}\:{equal} \\ $$$${to}\:\mathrm{1}.\:{but}\:{it}\:{has}\:{no}\:{minimum}\:{m},\:{i}.{e}. \\ $$$${m}={min}\left({f}\left({t}\right)\right)\:{doesn}'{t}\:{exist}.\:{if}\:{m} \\ $$$${doesn}'{t}\:{exist},\:{we}\:{can}\:{also}\:{not}\:{solve} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0},\:{because}\:{in}\:{this} \\ $$$${equation}\:{m}\:{is}\:{not}\:{just}\:{a}\:{variable},\:{but} \\ $$$${a}\:{concrete}\:{value}\:{which}\:{is}\:{defined}\:{as} \\ $$$${the}\:{minimum}\:{value}\:{of}\:{the}\:{function} \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }.\:{when}\:{m}\:{doesn}'{t}\:{exist}, \\ $$$${the}\:{so}\:{called}\:{roots}\:−\mathrm{1}\pm\sqrt{\mathrm{1}−{m}}\:{don}'{t} \\ $$$${exist}\:{either}. \\ $$$${in}\:{your}\:{question}\:{m}\:{is}\:{defined}\:{as} \\ $$$${the}\:{minimun}\:{of}\:{a}\:{function} \\ $$$${F}\left({a},{b},{c}\right).\:{but}\:{this}\:{function}\:{also}\:{has} \\ $$$${no}\:{minimum}\:{m},\:{therefore}\:{x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0} \\ $$$${has}\:{no}\:{roots}. \\ $$
Commented by HongKing last updated on 13/Nov/21

$$\boldsymbol{\mathrm{m}}\:\:\mathrm{is}\:\mathrm{constant},\:\mathrm{not}\:\mathrm{variable} \\ $$
Commented by mr W last updated on 13/Nov/21

$$\boldsymbol{\mathrm{m}}\:\:\mathrm{is}\:\mathrm{constant}\:{which}\:{doesn}'{t}\:{exist}. \\ $$$${this}\:{is}\:{elementary},\:{i}\:{think}\:{there}\:{is} \\ $$$${no}\:{need}\:{for}\:{further}\:{discussion}\:{about} \\ $$$${it}. \\ $$
Commented by HongKing last updated on 13/Nov/21

$$\mathrm{When}\:\mathrm{we}\:\mathrm{assume}\:\mathrm{that}\:\boldsymbol{\mathrm{m}}\:\mathrm{is}\:\mathrm{greater}, \\ $$$$\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{wrong}\:\mathrm{result}, \\ $$$$\mathrm{then}\:\boldsymbol{\mathrm{m}}\:\mathrm{must}\:\mathrm{be}\:\mathrm{less}\:\mathrm{1}, \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{main}\:\mathrm{idea}.. \\ $$
Commented by HongKing last updated on 13/Nov/21

$$\mathrm{Again}.. \\ $$$$\mathrm{The}\:\mathrm{equation}:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{m}=\mathrm{0}\:\rightarrow\:\mathrm{with}:\:\Delta=\mathrm{4}\left(\mathrm{1}-\mathrm{n}\right) \\ $$$$\mathrm{Assume}\:\mathrm{that}:\:\:\mathrm{m}>\mathrm{1}\:\rightarrow\:\mathrm{then}:\:\mathrm{2ab}^{\mathrm{2}} +\mathrm{b}^{\mathrm{3}} \mathrm{c}>\mathrm{1}\:;\:\mathrm{2bc}^{\mathrm{2}} +\mathrm{c}^{\mathrm{3}} \mathrm{a}>\mathrm{1}\:;\:\mathrm{2ca}^{\mathrm{2}} +\mathrm{a}^{\mathrm{3}} \mathrm{b}>\mathrm{1} \\ $$$$\mathrm{Now}\:\mathrm{using}\:\mathrm{condition}:\:\:\mathrm{2ab}^{\mathrm{2}} +\mathrm{b}^{\mathrm{3}} \mathrm{c}=\mathrm{b}^{\mathrm{2}} \left(\mathrm{2}\left(\mathrm{2}-\mathrm{b}-\mathrm{c}\right)+\mathrm{bc}\right)=\mathrm{b}^{\mathrm{2}} \left(\mathrm{2}-\mathrm{b}\right)\left(\mathrm{2}-\mathrm{c}\right)>\mathrm{1} \\ $$$$\mathrm{Smilarly}:\:\:\mathrm{2bc}^{\mathrm{2}} +\mathrm{c}^{\mathrm{3}} \mathrm{a}=\mathrm{c}^{\mathrm{2}} \left(\mathrm{2}-\mathrm{a}\right)\left(\mathrm{2}-\mathrm{c}\right)>\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2ca}^{\mathrm{2}} +\mathrm{a}^{\mathrm{3}} \mathrm{b}=\mathrm{a}^{\mathrm{2}} \left(\mathrm{2}-\mathrm{a}\right)\left(\mathrm{2}-\mathrm{b}\right)>\mathrm{1} \\ $$$$\mathrm{Thus}:\:\:\mathrm{abc}\left(\mathrm{2}-\mathrm{a}\right)\left(\mathrm{2}-\mathrm{b}\right)\left(\mathrm{2}-\mathrm{c}\right)>\mathrm{1}\:\:\left(\ast\right) \\ $$$$\mathrm{Using}\:\boldsymbol{\mathrm{AM}}-\boldsymbol{\mathrm{GM}}\:\rightarrow\:\:\mathrm{0}\leqslant\mathrm{a}\left(\mathrm{2}-\mathrm{a}\right)\leqslant\mathrm{1}\:;\:\mathrm{0}\leqslant\mathrm{b}\left(\mathrm{2}-\mathrm{b}\right)\leqslant\mathrm{1}\:;\:\mathrm{0}\leqslant\mathrm{c}\left(\mathrm{2}-\mathrm{c}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{Or}:\:\:\mathrm{abc}\left(\mathrm{2}-\mathrm{a}\right)\left(\mathrm{2}-\mathrm{b}\right)\left(\mathrm{2}-\mathrm{c}\right)\leqslant\mathrm{1}\:\:\left(\ast\ast\right) \\ $$$$\mathrm{By}\:\left(\ast\right)\:\mathrm{and}\:\left(\ast\ast\right)\:\mathrm{we}\:\mathrm{get}\:\:\boldsymbol{\mathrm{m}}\leqslant\mathrm{1}\:\:\mathrm{and}\:\mathrm{the}\:\mathrm{initial}\:\:\mathrm{equation}\:\mathrm{has}\:\mathrm{root}: \\ $$$$\boldsymbol{\mathrm{x}}_{\mathrm{1}} \:;\:\boldsymbol{\mathrm{x}}_{\mathrm{2}} \:=\:\left\{-\mathrm{1}\:+\:\sqrt{\mathrm{1}\:-\:\mathrm{m}}\:;\:-\mathrm{1}\:-\:\sqrt{\mathrm{1}\:-\:\mathrm{m}}\:\right\} \\ $$
Commented by mr W last updated on 13/Nov/21

$${even}\:{when}\:{m}>\mathrm{1}\:{there}\:{are}\:{roots}\:{from} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0}.\:{but}\:{even}\:{whem}\:{m}<\mathrm{1}, \\ $$$${but}\:{when}\:{it}\:{doesn}'{t}\:{exist},\:{there}\:{is}\:{no} \\ $$$${root}\:{from}\:{x}^{\mathrm{2}} +\mathrm{2}{x}+{m}=\mathrm{0}.\:{i}'{m}\:{only} \\ $$$${convinced}\:{when}\:{you}\:{can}\:{find}\:{the} \\ $$$${minimum}\:{value}\:{m}\:{concretely}.\:{the} \\ $$$${minimum}\:{of}\:{a}\:{function}\:{is}\:{a}\:{fixed} \\ $$$${value},\:{not}\:{a}\:{range}\:{like}\:{m}\leqslant\mathrm{1}. \\ $$
