Question Number 68068 by mhmd last updated on 04/Sep/19
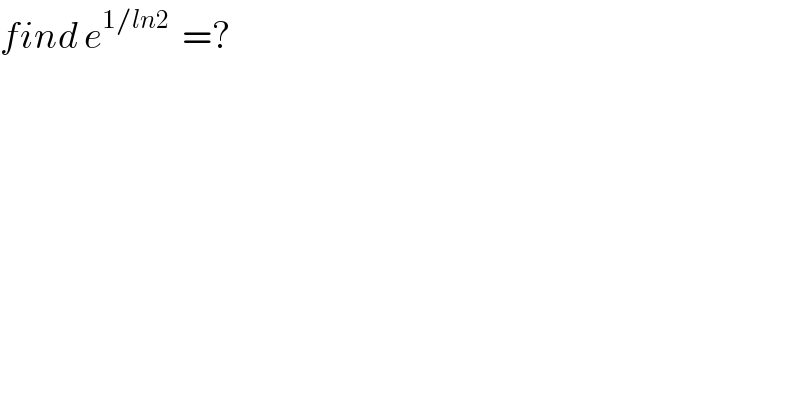
$${find}\:{e}^{\mathrm{1}/{ln}\mathrm{2}} \:\:=? \\ $$
Commented by peter frank last updated on 04/Sep/19
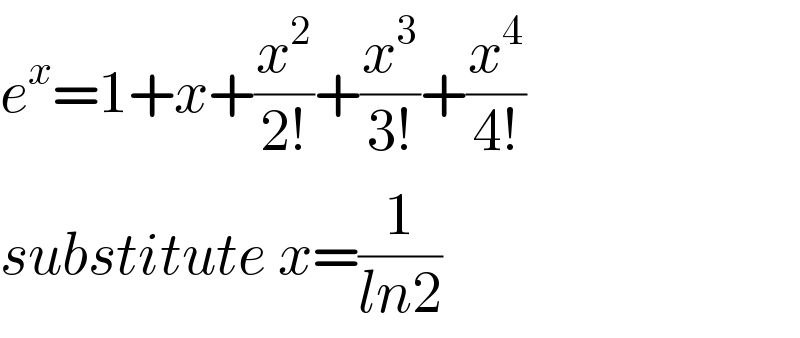
$${e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!} \\ $$$${substitute}\:{x}=\frac{\mathrm{1}}{{ln}\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 04/Sep/19
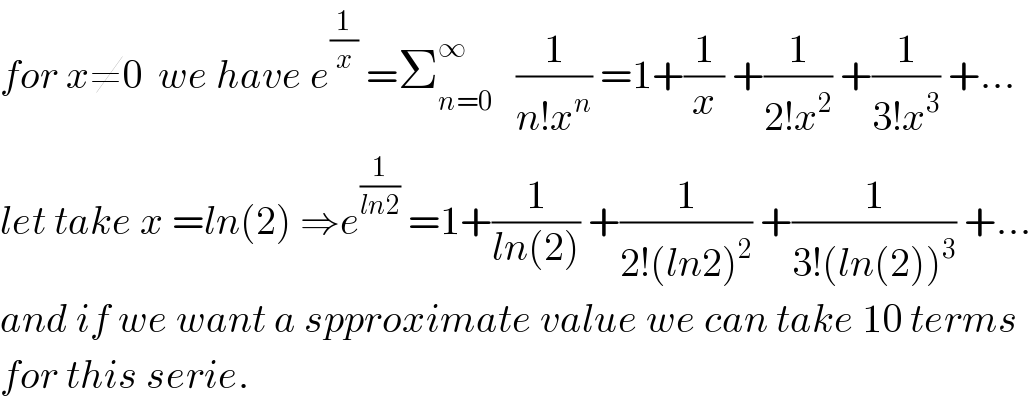
$${for}\:{x}\neq\mathrm{0}\:\:{we}\:{have}\:{e}^{\frac{\mathrm{1}}{{x}}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}!{x}^{{n}} }\:=\mathrm{1}+\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{\mathrm{2}!{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{3}} }\:+… \\ $$$${let}\:{take}\:{x}\:={ln}\left(\mathrm{2}\right)\:\Rightarrow{e}^{\frac{\mathrm{1}}{{ln}\mathrm{2}}} \:=\mathrm{1}+\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}!\left({ln}\mathrm{2}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{3}!\left({ln}\left(\mathrm{2}\right)\right)^{\mathrm{3}} }\:+… \\ $$$${and}\:{if}\:{we}\:{want}\:{a}\:{spproximate}\:{value}\:{we}\:{can}\:{take}\:\mathrm{10}\:{terms} \\ $$$${for}\:{this}\:{serie}. \\ $$
