Question Number 28050 by ajfour last updated on 19/Jan/18

Commented by ajfour last updated on 19/Jan/18

$${The}\:{blue}\:{disc},\:{radius}\:\boldsymbol{{r}},{mass}\:\boldsymbol{{m}}, \\ $$$${rolls}\:{on}\:{the}\:{ground}\:{in}\:{a}\:{circle}\:{of} \\ $$$${radius}\:\boldsymbol{{R}}.\:{It}\:{rolls}\:{and}\:{its}\:{axis} \\ $$$${maintains}\:{a}\:{constant}\:{angle}\:{with} \\ $$$${the}\:{horizontal}\:{plane}.\:{Assuming} \\ $$$${no}\:{energy}\:{losses}\:{therefore},\:{find} \\ $$$${its}\:{kinetic}\:{energy}. \\ $$
Commented by mrW2 last updated on 19/Jan/18
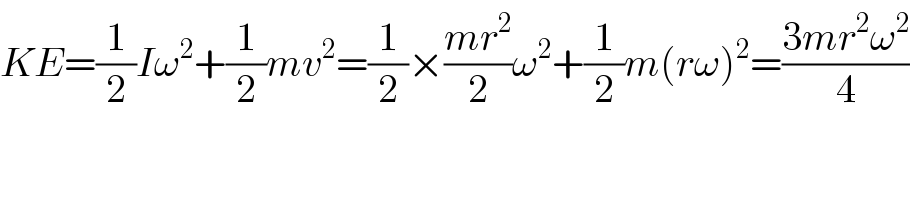
$${KE}=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left({r}\omega\right)^{\mathrm{2}} =\frac{\mathrm{3}{mr}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by ajfour last updated on 19/Jan/18

$${Find}\:\omega\:{also}\:{if}\:{the}\:{disc}\:{has}\:{to}\:{keep} \\ $$$${rolling}\:{in}\:{the}\:{circle}\:{of}\:{radius}\:{R}, \\ $$$${Sir}.{The}\:{disc}\:{is}\:{thin},\:{its}\:{axis}\:{is} \\ $$$${bent}\:{by}\:{some}\:{acute}\:{angle}.\: \\ $$$${Further}\:{we}\:{have}\:{two}\:\omega\:{types}.. \\ $$
Commented by mrW2 last updated on 19/Jan/18
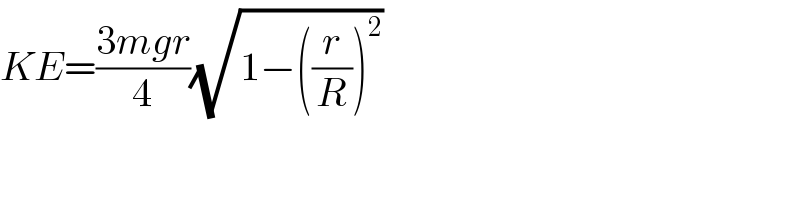
$${KE}=\frac{\mathrm{3}{mgr}}{\mathrm{4}}\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 19/Jan/18

$${cannot}\:{confirm}\:{Sir},\:{the}\:{question} \\ $$$${occured}\:{to}\:{me}\:{seeing}\:{a}\:{little}\: \\ $$$${similar}\:{one}\:{in}\:{a}\:{book}. \\ $$$${Please}\:{explain}. \\ $$
Commented by mrW2 last updated on 19/Jan/18
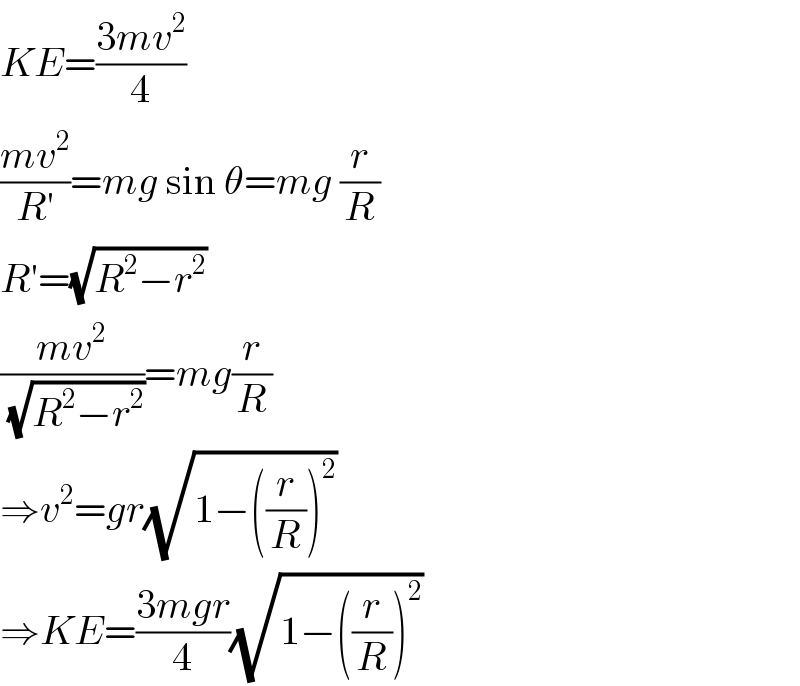
$${KE}=\frac{\mathrm{3}{mv}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{{mv}^{\mathrm{2}} }{{R}'}={mg}\:\mathrm{sin}\:\theta={mg}\:\frac{{r}}{{R}} \\ $$$${R}'=\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\frac{{mv}^{\mathrm{2}} }{\:\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }}={mg}\frac{{r}}{{R}} \\ $$$$\Rightarrow{v}^{\mathrm{2}} ={gr}\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{KE}=\frac{\mathrm{3}{mgr}}{\mathrm{4}}\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} } \\ $$
Commented by mrW2 last updated on 19/Jan/18
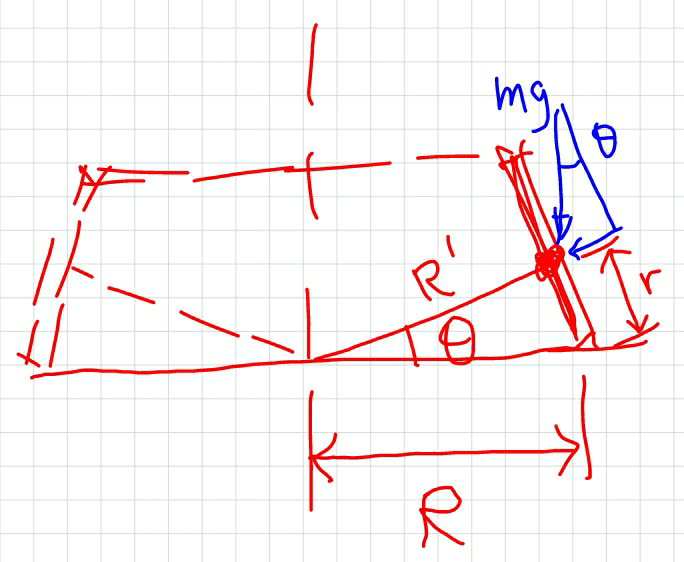
Commented by ajfour last updated on 19/Jan/18
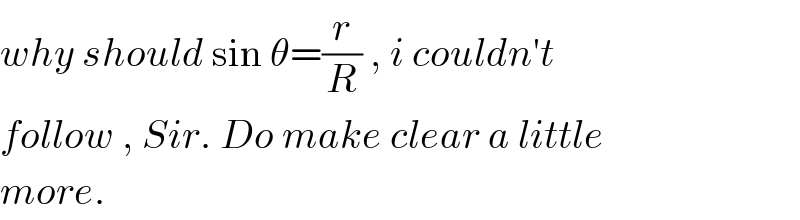
$${why}\:{should}\:\mathrm{sin}\:\theta=\frac{{r}}{{R}}\:,\:{i}\:{couldn}'{t} \\ $$$${follow}\:,\:{Sir}.\:{Do}\:{make}\:{clear}\:{a}\:{little} \\ $$$${more}. \\ $$
Commented by mrW2 last updated on 19/Jan/18
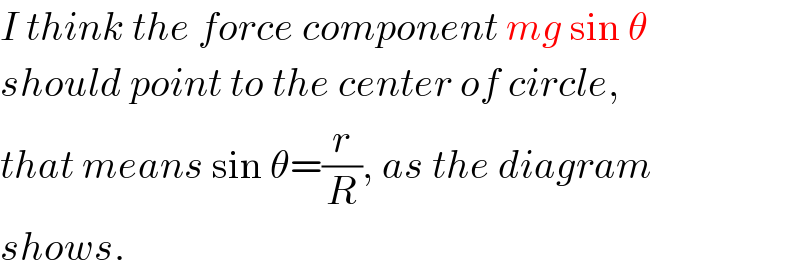
$${I}\:{think}\:{the}\:{force}\:{component}\:{mg}\:\mathrm{sin}\:\theta \\ $$$${should}\:{point}\:{to}\:{the}\:{center}\:{of}\:{circle}, \\ $$$${that}\:{means}\:\mathrm{sin}\:\theta=\frac{{r}}{{R}},\:{as}\:{the}\:{diagram} \\ $$$${shows}. \\ $$
Commented by ajfour last updated on 19/Jan/18
$${good}\:{clue},\:{Sir}.\:{Thank}\:{you}. \\ $$
Commented by ajfour last updated on 20/Jan/18

$${but}\:{in}\:{one}\:{revolution},\:{there}\:{is}\:{one} \\ $$$${rotation}\:{even}\:{of}\:{the}\:{disc}\:{about} \\ $$$${vertical}\:{axis},\:{Sir}\:! \\ $$
Commented by mrW2 last updated on 20/Jan/18
)^2 ))](https://www.tinkutara.com/question/Q28081.png)
$${Yes}.\:{I}\:{noticed}\:{this}\:{too}.\:{The}\:{disc}\:{makes} \\ $$$${one}\:{rotation}\:{about}\:{its}\:{vertical}\:{axis}\: \\ $$$${when}\:{it}\:{rolls}\:{a}\:{round}\:{alone}\:{the}\:{circle}. \\ $$$${The}\:{angular}\:{speed}\:{is}\:\omega_{\mathrm{3}} =\frac{\mathrm{2}\pi}{\frac{\mathrm{2}\pi{R}}{{v}}}=\frac{{v}}{{R}}=\frac{\omega_{\mathrm{1}} {r}}{{R}}, \\ $$$${the}\:{corresponding}\:{KE}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{3}} \omega_{\mathrm{3}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mr}^{\mathrm{2}} }{\mathrm{4}}×\frac{{v}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{{mgr}^{\mathrm{3}} }{\mathrm{8}{R}^{\mathrm{2}} }\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{KE}_{{total}} =\frac{{mgr}}{\mathrm{8}}\left[\mathrm{6}+\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} \right]\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 20/Jan/18

$${If}\:{it}\:{is}\:{correct}\:,\:{really}\:{wondurful} \\ $$$${Sir},\:{i}\:{am}\:{amazed}! \\ $$
Commented by ajfour last updated on 20/Jan/18
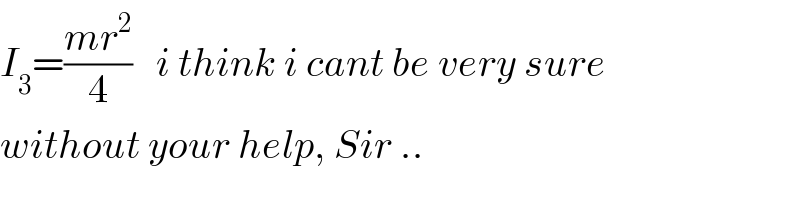
$${I}_{\mathrm{3}} =\frac{{mr}^{\mathrm{2}} }{\mathrm{4}}\:\:\:{i}\:{think}\:{i}\:{cant}\:{be}\:{very}\:{sure} \\ $$$${without}\:{your}\:{help},\:{Sir}\:.. \\ $$
