Question Number 28124 by ajfour last updated on 20/Jan/18
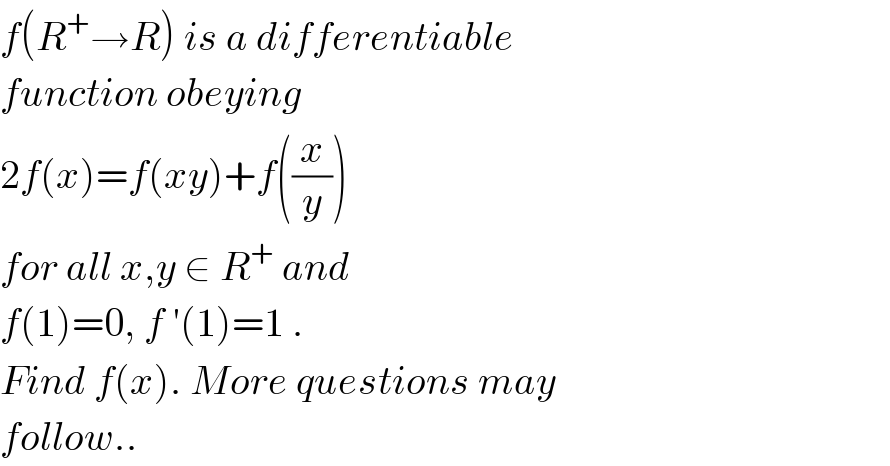
$${f}\left({R}^{+} \rightarrow{R}\right)\:{is}\:{a}\:{differentiable} \\ $$$${function}\:{obeying} \\ $$$$\mathrm{2}{f}\left({x}\right)={f}\left({xy}\right)+{f}\left(\frac{{x}}{{y}}\right) \\ $$$${for}\:{all}\:{x},{y}\:\in\:{R}^{+} \:{and}\: \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0},\:{f}\:'\left(\mathrm{1}\right)=\mathrm{1}\:. \\ $$$${Find}\:{f}\left({x}\right).\:{More}\:{questions}\:{may} \\ $$$${follow}.. \\ $$
Commented by prakash jain last updated on 20/Jan/18

$${y}={x} \\ $$$${f}\left({x}^{\mathrm{2}} \right)=\mathrm{2}{f}\left({x}\right) \\ $$$${f}\left({x}\right)={c}\mathrm{ln}\:{x} \\ $$$${check} \\ $$$$\mathrm{2}{c}\mathrm{ln}\:{x}={c}\mathrm{ln}\:{x}+{c}\mathrm{ln}\:{y}+{c}\mathrm{ln}\:{x}−{c}\mathrm{ln}\:{y} \\ $$$${f}'\left({x}\right)=\frac{{c}}{{x}} \\ $$$${f}'\left(\mathrm{1}\right)=\mathrm{1}\Rightarrow{c}=\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{ln}\:{x} \\ $$
Commented by ajfour last updated on 20/Jan/18

$${Are}\:{the}\:{following}\:{true}: \\ $$$$\left({i}\right)\:{No}.\:{of}\:{solutions}\:{of}\:{f}^{\:−\mathrm{1}} \left({x}\right)={x}^{\mathrm{5}} \\ $$$${is}\:\mathrm{3} \\ $$$$\left({ii}\right){there}\:{is}\:{at}\:{least}\:{one}\:{point}\:\alpha\in \\ $$$$\left(\mathrm{0},\infty\right)\:{for}\:{which}\:{f}^{\:−\mathrm{1}} \left({x}\right)−{x}^{\mathrm{5}} \:>\:\mathrm{0} \\ $$$${for}\:{x}\in\:\left(\alpha,\infty\right)\:? \\ $$
Commented by ajfour last updated on 20/Jan/18

$${thank}\:{you}\:{Sir}. \\ $$
