Question Number 28268 by abdo imad last updated on 22/Jan/18
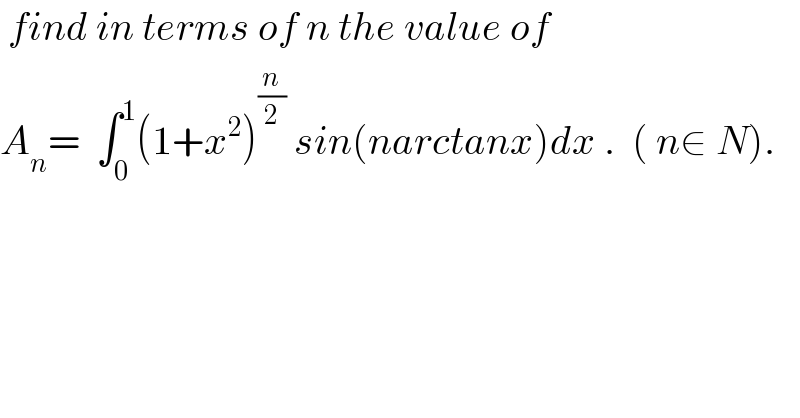
$$\:{find}\:{in}\:{terms}\:{of}\:{n}\:{the}\:{value}\:{of} \\ $$$${A}_{{n}} =\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{{n}}{\mathrm{2}}} \:{sin}\left({narctanx}\right){dx}\:.\:\:\left(\:{n}\in\:{N}\right). \\ $$
Commented by abdo imad last updated on 23/Jan/18
![let introduce the polynome P(x)= (1/(2i)) ((1+ix)^n −(1−ix)^n ) let write P(x) in geometric form .we have ∣1+ix∣= (√(1+x^2 ))= (1+x^2 )^(1/2) and 1+ix = (√(1+x^2 )) ( (1/( (√(1+x^2 )))) +i(x/( (√(1+x^2 )))))= r e^(iθ) ⇒ r=(√(1+x^2 )) and tanθ=x⇒ θ=artanx so (1+ix)^n = (1+x^2 )^(n/2) e^(inarctanx) (1−ix)^n =(1+x^2 )^(n/2) e^(−inartanx) and P(x)=(1/(2i))( 2iIm((1+ix)^n ))= (1+x^2 )^(n/2) sin(narctanx) ⇒ A_n =∫_0 ^1 P(x)dx but we have proved that P(x)= Σ_(p=0) ^([((n−1)/2)]) (−1)^p C_n ^(2p+1) x^(2p+1) ∫_0 ^1 P(x)dx = Σ_(p=0) ^([((n−1)/2)]) (−1)^p (C_n ^(2p+1) /(2p+2)) = A_n .](https://www.tinkutara.com/question/Q28282.png)
$${let}\:{introduce}\:{the}\:{polynome}\:{P}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\:\left(\left(\mathrm{1}+{ix}\right)^{{n}} \:−\left(\mathrm{1}−{ix}\right)^{{n}} \right) \\ $$$${let}\:{write}\:{P}\left({x}\right)\:{in}\:{geometric}\:{form}\:\:.{we}\:{have}\: \\ $$$$\mid\mathrm{1}+{ix}\mid=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }=\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{and} \\ $$$$\mathrm{1}+{ix}\:=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\left(\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+{i}\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)=\:{r}\:{e}^{{i}\theta} \:\:\Rightarrow \\ $$$${r}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:{and}\:\:{tan}\theta={x}\Rightarrow\:\theta={artanx}\:\:{so} \\ $$$$\left(\mathrm{1}+{ix}\right)^{{n}} =\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{{n}}{\mathrm{2}}} \:{e}^{{inarctanx}} \:\: \\ $$$$\left(\mathrm{1}−{ix}\right)^{{n}} =\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{{n}}{\mathrm{2}}} \:{e}^{−{inartanx}} \:\:{and} \\ $$$${P}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\:\mathrm{2}{iIm}\left(\left(\mathrm{1}+{ix}\right)^{{n}} \right)\right)=\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{{n}}{\mathrm{2}}} \:{sin}\left({narctanx}\right) \\ $$$$\Rightarrow\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {P}\left({x}\right){dx}\:\:\:{but}\:{we}\:{have}\:{proved}\:{that} \\ $$$${P}\left({x}\right)=\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\left(−\mathrm{1}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:{x}^{\mathrm{2}{p}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {P}\left({x}\right){dx}\:=\:\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\left(−\mathrm{1}\right)^{{p}} \:\:\frac{{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} }{\mathrm{2}{p}+\mathrm{2}}\:=\:{A}_{{n}} \:\:. \\ $$
