Question Number 68094 by mhmd last updated on 04/Sep/19
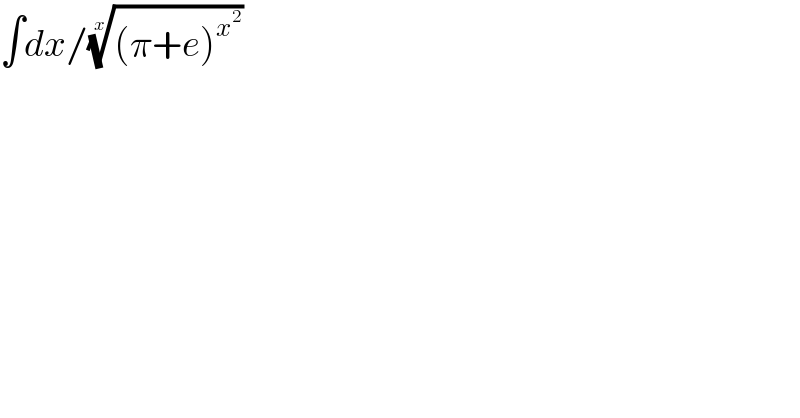
$$\int{dx}/\sqrt[{{x}}]{\left(\pi+{e}\right)^{{x}^{\mathrm{2}} } }\: \\ $$
Answered by MJS last updated on 05/Sep/19
![∫(dx/( (((π+e)^x^2 ))^(1/x) ))=∫(dx/((π+e)^x ))=−(1/((π+e)^x ln (π+e)))+C [∫a^x dx=(a^x /(ln a)); a=(π+e)^(−1) ]](https://www.tinkutara.com/question/Q68112.png)
$$\int\frac{{dx}}{\:\sqrt[{{x}}]{\left(\pi+\mathrm{e}\right)^{{x}^{\mathrm{2}} } }}=\int\frac{{dx}}{\left(\pi+\mathrm{e}\right)^{{x}} }=−\frac{\mathrm{1}}{\left(\pi+\mathrm{e}\right)^{{x}} \:\mathrm{ln}\:\left(\pi+\mathrm{e}\right)}+{C} \\ $$$$\:\:\:\:\:\left[\int{a}^{{x}} {dx}=\frac{{a}^{{x}} }{\mathrm{ln}\:{a}};\:{a}=\left(\pi+\mathrm{e}\right)^{−\mathrm{1}} \right] \\ $$
