Menu Close

Find-lim-x-0-5x-tan-5x-x-3-

Tinku Tara 0 Comments
Pin




Question Number 28341 by Cheyboy last updated on 24/Jan/18
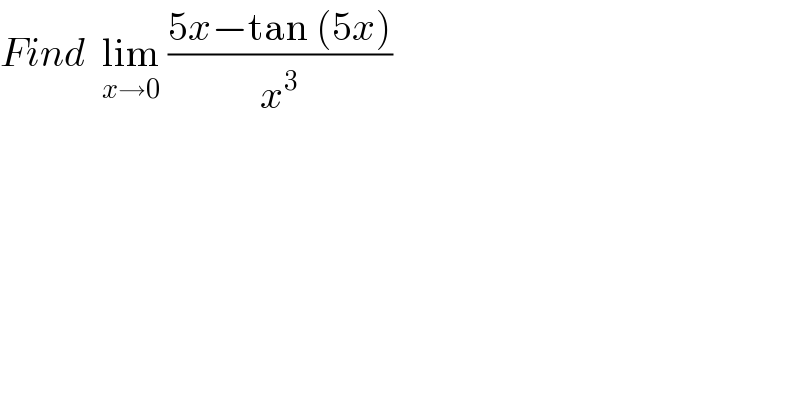
Find lim_(x→0) ((5x−tan (5x))/x^3 )
$${Find}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}{x}−\mathrm{tan}\:\left(\mathrm{5}{x}\right)}{{x}^{\mathrm{3}} } \\ $$
Commented by Cheyboy last updated on 24/Jan/18
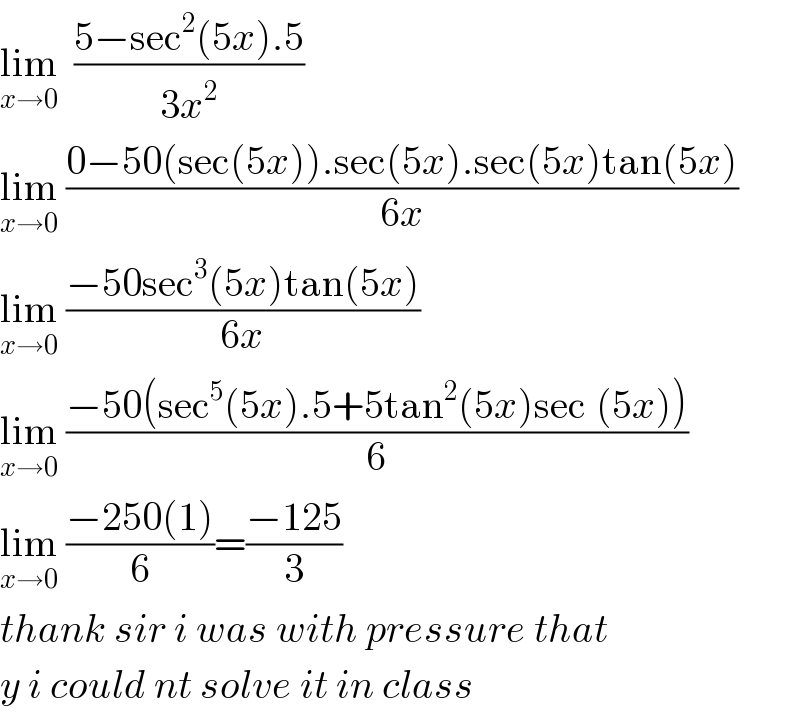
lim_(x→0) ((5−sec^2 (5x).5)/(3x^2 )) lim_(x→0) ((0−50(sec(5x)).sec(5x).sec(5x)tan(5x))/(6x)) lim_(x→0) ((−50sec^3 (5x)tan(5x))/(6x)) lim_(x→0) ((−50(sec^5 (5x).5+5tan^2 (5x)sec^ (5x)))/6) lim_(x→0) ((−250(1))/6)=((−125)/3) thank sir i was with pressure that y i could nt solve it in class
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{5}−\mathrm{sec}^{\mathrm{2}} \left(\mathrm{5}{x}\right).\mathrm{5}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{0}−\mathrm{50}\left(\mathrm{sec}\left(\mathrm{5}{x}\right)\right).\mathrm{sec}\left(\mathrm{5}{x}\right).\mathrm{sec}\left(\mathrm{5}{x}\right)\mathrm{tan}\left(\mathrm{5}{x}\right)}{\mathrm{6}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{50sec}^{\mathrm{3}} \left(\mathrm{5}{x}\right)\mathrm{tan}\left(\mathrm{5}{x}\right)}{\mathrm{6}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{50}\left(\mathrm{sec}^{\mathrm{5}} \left(\mathrm{5}{x}\right).\mathrm{5}+\mathrm{5tan}^{\mathrm{2}} \left(\mathrm{5}{x}\right)\mathrm{sec}^{} \left(\mathrm{5}{x}\right)\right)}{\mathrm{6}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{250}\left(\mathrm{1}\right)}{\mathrm{6}}=\frac{−\mathrm{125}}{\mathrm{3}} \\ $$$${thank}\:{sir}\:{i}\:{was}\:{with}\:{pressure}\:{that} \\ $$$${y}\:{i}\:{could}\:{nt}\:{solve}\:{it}\:{in}\:{class} \\ $$
Commented by abdo imad last updated on 25/Jan/18
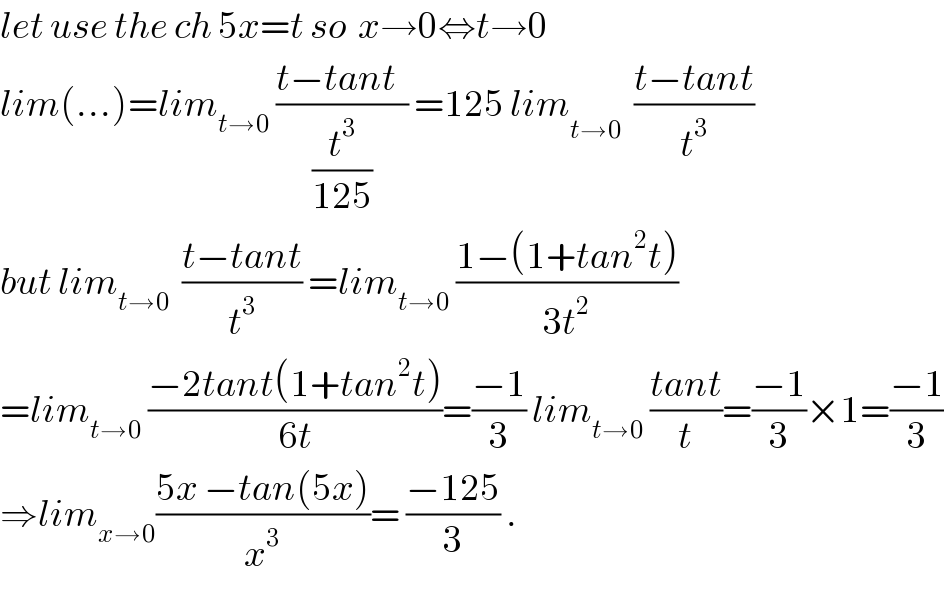
let use the ch 5x=t so x→0⇔t→0 lim(...)=lim_(t→0) ((t−tant )/(t^3 /(125))) =125 lim_(t→0^ ) ((t−tant)/t^3 ) but lim_(t→0) ((t−tant)/t^3 ) =lim_(t→0) ((1−(1+tan^2 t))/(3t^2 )) =lim_(t→0) ((−2tant(1+tan^2 t))/(6t))=((−1)/3) lim_(t→0) ((tant)/t)=((−1)/3)×1=((−1)/3) ⇒lim_(x→0) ((5x −tan(5x))/x^3 )= ((−125)/3) .
$${let}\:{use}\:{the}\:{ch}\:\mathrm{5}{x}={t}\:{so}\:\:{x}\rightarrow\mathrm{0}\Leftrightarrow{t}\rightarrow\mathrm{0} \\ $$$${lim}\left(…\right)={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{t}−{tant}\:\:}{\frac{{t}^{\mathrm{3}} }{\mathrm{125}}}\:=\mathrm{125}\:{lim}_{{t}\rightarrow\mathrm{0}^{\:} \:} \:\frac{{t}−{tant}}{{t}^{\mathrm{3}} } \\ $$$${but}\:{lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{{t}−{tant}}{{t}^{\mathrm{3}} }\:={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)}{\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{−\mathrm{2}{tant}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)}{\mathrm{6}{t}}=\frac{−\mathrm{1}}{\mathrm{3}}\:{lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{tant}}{{t}}=\frac{−\mathrm{1}}{\mathrm{3}}×\mathrm{1}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{5}{x}\:−{tan}\left(\mathrm{5}{x}\right)}{{x}^{\mathrm{3}} }=\:\frac{−\mathrm{125}}{\mathrm{3}}\:. \\ $$
Commented by abdo imad last updated on 25/Jan/18
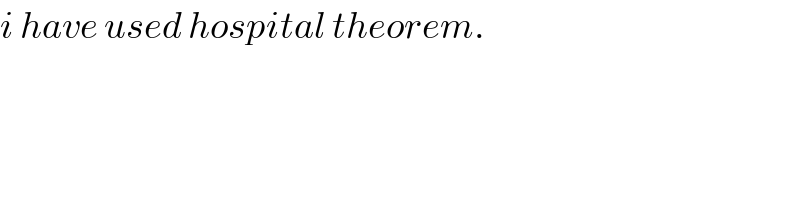
i have used hospital theorem.
$${i}\:{have}\:{used}\:{hospital}\:{theorem}. \\ $$
Commented by Cheyboy last updated on 25/Jan/18
Thank sir God bless you =
$${Thank}\:{sir}\:{God}\:{bless}\:{you} \\ $$$$= \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 24/Jan/18
=lim_(x→0) ((5x−(5x+(((5x)^3 )/3)+((2(5x)^5 )/(15))+...))/x^3 ) =lim_(x→0) ((−((125)/3)+((2×125)/(15))(5x)^2 )/1) = − ((125)/3) .
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}{x}−\left(\mathrm{5}{x}+\frac{\left(\mathrm{5}{x}\right)^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}\left(\mathrm{5}{x}\right)^{\mathrm{5}} }{\mathrm{15}}+…\right)}{{x}^{\mathrm{3}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{125}}{\mathrm{3}}+\frac{\mathrm{2}×\mathrm{125}}{\mathrm{15}}\left(\mathrm{5}{x}\right)^{\mathrm{2}} }{\mathrm{1}}\: \\ $$$$=\:\:−\:\frac{\mathrm{125}}{\mathrm{3}}\:. \\ $$
Commented by Cheyboy last updated on 24/Jan/18
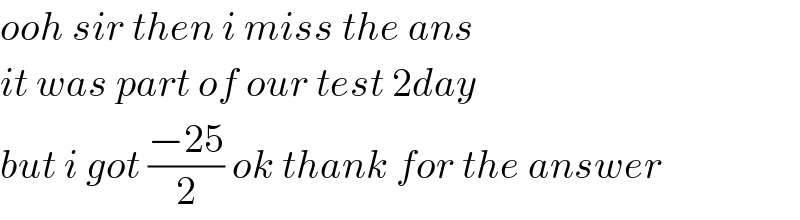
ooh sir then i miss the ans it was part of our test 2day but i got ((−25)/2) ok thank for the answer
$${ooh}\:{sir}\:{then}\:{i}\:{miss}\:{the}\:{ans} \\ $$$${it}\:{was}\:{part}\:{of}\:{our}\:{test}\:\mathrm{2}{day}\: \\ $$$${but}\:{i}\:{got}\:\frac{−\mathrm{25}}{\mathrm{2}}\:{ok}\:{thank}\:{for}\:{the}\:{answer} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *