Question Number 93904 by i jagooll last updated on 16/May/20
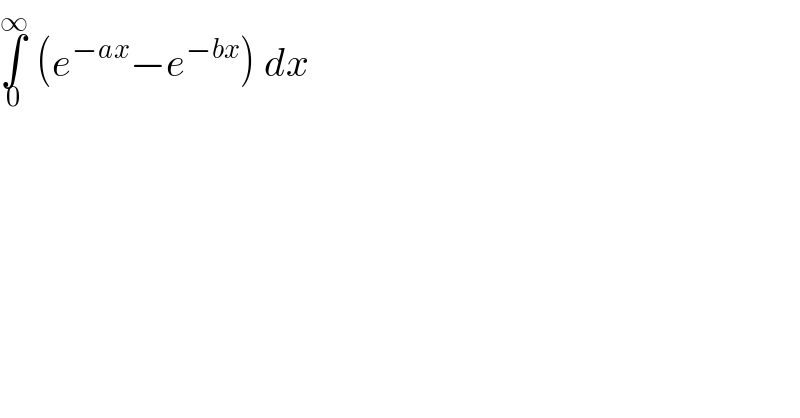
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\left({e}^{−{ax}} −{e}^{−{bx}} \right)\:{dx}\: \\ $$
Answered by i jagooll last updated on 16/May/20
![= lim_(p→∞) ∫_0 ^p (e^(−ax) −e^(−bx) )dx = lim_(p→∞) [ −(1/a)e^(−ax) +(1/b)e^(−bx) ] _0 ^p = 0−[−(1/a)+(1/b)]= (1/a)−(1/b) = ((b−a)/(ab))](https://www.tinkutara.com/question/Q93905.png)
$$=\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{0}} {\overset{{p}} {\int}}\:\left({e}^{−{ax}} −{e}^{−{bx}} \right){dx} \\ $$$$=\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\left[\:−\frac{\mathrm{1}}{{a}}{e}^{−{ax}} +\frac{\mathrm{1}}{{b}}{e}^{−{bx}} \:\right]\underset{\mathrm{0}} {\overset{{p}} {\:}} \\ $$$$=\:\mathrm{0}−\left[−\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right]=\:\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{b}} \\ $$$$=\:\frac{{b}−{a}}{{ab}} \\ $$
