Question Number 159527 by HongKing last updated on 18/Nov/21

Commented by mr W last updated on 18/Nov/21

$${only}\:{x}=\frac{\mathrm{23}}{\mathrm{24}} \\ $$
Commented by HongKing last updated on 18/Nov/21
$$\mathrm{yes}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{but}\:\mathrm{solution}\:\mathrm{if}\:\mathrm{possible}\:\mathrm{please} \\ $$
Answered by mr W last updated on 18/Nov/21
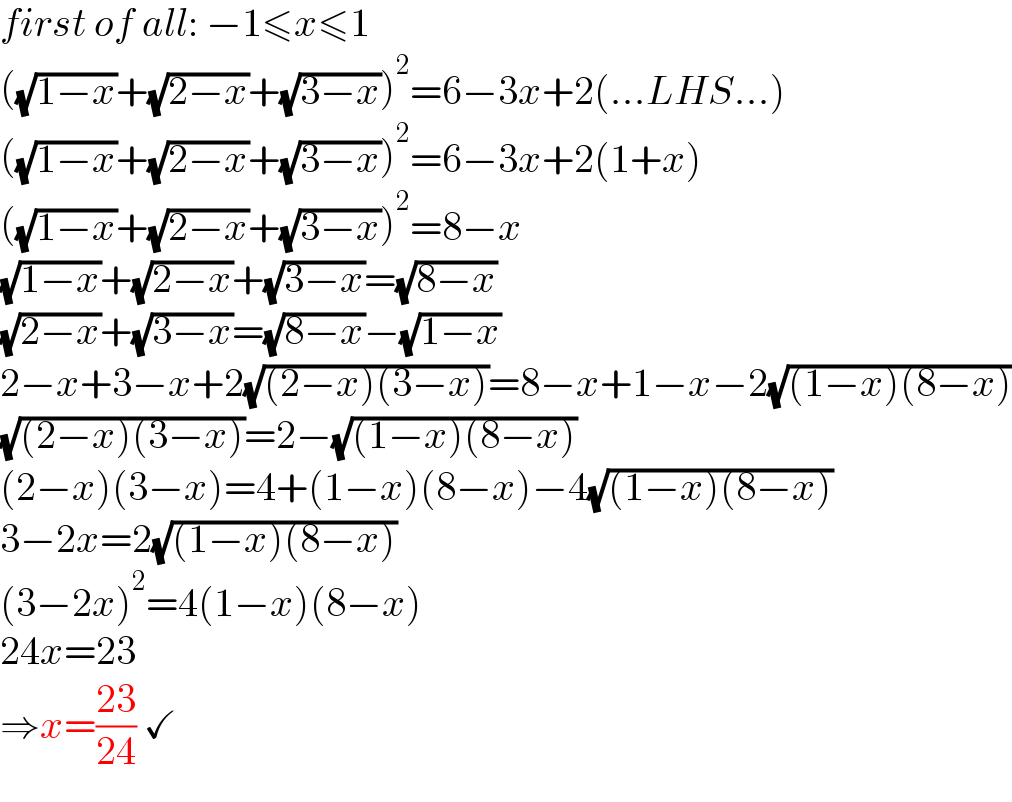
$${first}\:{of}\:{all}:\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$$\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{2}−{x}}+\sqrt{\mathrm{3}−{x}}\right)^{\mathrm{2}} =\mathrm{6}−\mathrm{3}{x}+\mathrm{2}\left(…{LHS}…\right) \\ $$$$\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{2}−{x}}+\sqrt{\mathrm{3}−{x}}\right)^{\mathrm{2}} =\mathrm{6}−\mathrm{3}{x}+\mathrm{2}\left(\mathrm{1}+{x}\right) \\ $$$$\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{2}−{x}}+\sqrt{\mathrm{3}−{x}}\right)^{\mathrm{2}} =\mathrm{8}−{x} \\ $$$$\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{2}−{x}}+\sqrt{\mathrm{3}−{x}}=\sqrt{\mathrm{8}−{x}} \\ $$$$\sqrt{\mathrm{2}−{x}}+\sqrt{\mathrm{3}−{x}}=\sqrt{\mathrm{8}−{x}}−\sqrt{\mathrm{1}−{x}} \\ $$$$\mathrm{2}−{x}+\mathrm{3}−{x}+\mathrm{2}\sqrt{\left(\mathrm{2}−{x}\right)\left(\mathrm{3}−{x}\right)}=\mathrm{8}−{x}+\mathrm{1}−{x}−\mathrm{2}\sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right)} \\ $$$$\sqrt{\left(\mathrm{2}−{x}\right)\left(\mathrm{3}−{x}\right)}=\mathrm{2}−\sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right)} \\ $$$$\left(\mathrm{2}−{x}\right)\left(\mathrm{3}−{x}\right)=\mathrm{4}+\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right)−\mathrm{4}\sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right)} \\ $$$$\mathrm{3}−\mathrm{2}{x}=\mathrm{2}\sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right)} \\ $$$$\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{x}\right)\left(\mathrm{8}−{x}\right) \\ $$$$\mathrm{24}{x}=\mathrm{23} \\ $$$$\Rightarrow{x}=\frac{\mathrm{23}}{\mathrm{24}}\:\checkmark \\ $$
Commented by HongKing last updated on 18/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{cool} \\ $$
