Question Number 28490 by A1B1C1D1 last updated on 26/Jan/18
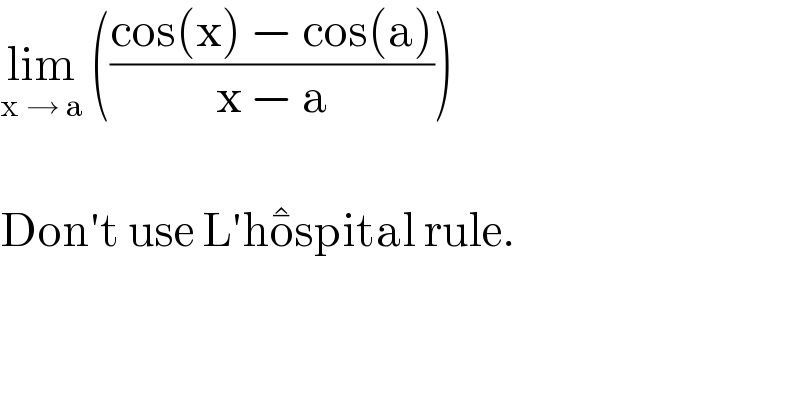
$$\underset{\mathrm{x}\:\rightarrow\:\mathrm{a}} {\mathrm{lim}}\:\left(\frac{\mathrm{cos}\left(\mathrm{x}\right)\:−\:\mathrm{cos}\left(\mathrm{a}\right)}{\mathrm{x}\:−\:\mathrm{a}}\right) \\ $$$$ \\ $$$$\mathrm{Don}'\mathrm{t}\:\mathrm{use}\:\mathrm{L}'\mathrm{h}\bar {\mathrm{o}spital}\:\mathrm{rule}. \\ $$
Answered by $@ty@m last updated on 27/Jan/18
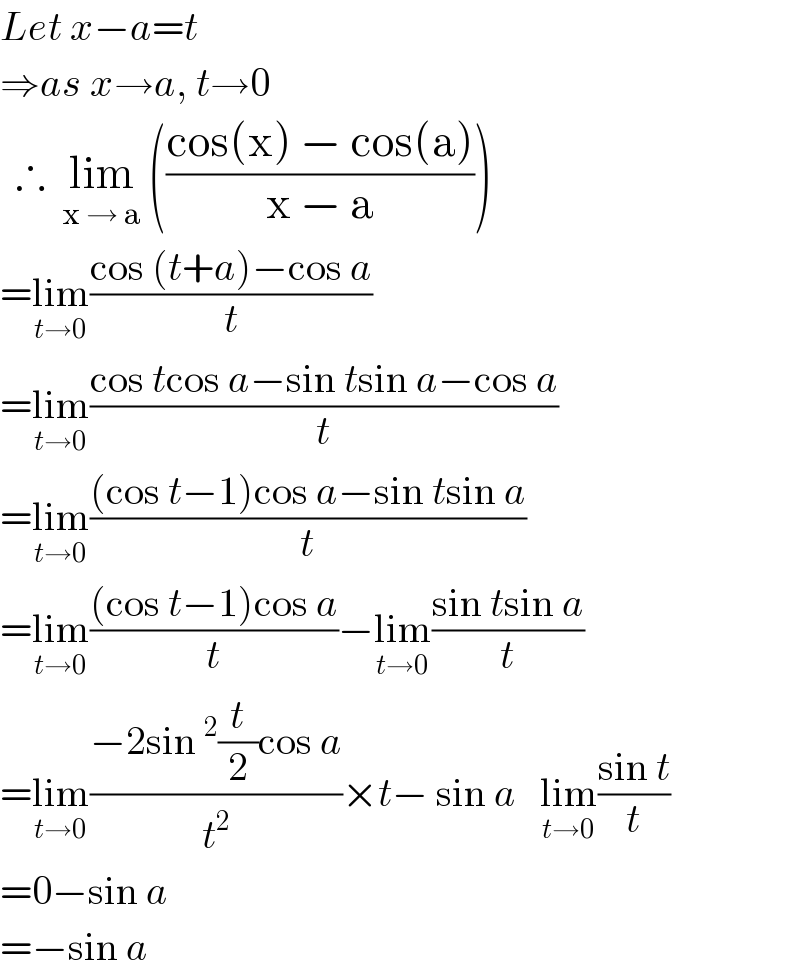
$${Let}\:{x}−{a}={t} \\ $$$$\Rightarrow{as}\:{x}\rightarrow{a},\:{t}\rightarrow\mathrm{0} \\ $$$$\:\:\therefore\:\:\underset{\mathrm{x}\:\rightarrow\:\mathrm{a}} {\mathrm{lim}}\:\left(\frac{\mathrm{cos}\left(\mathrm{x}\right)\:−\:\mathrm{cos}\left(\mathrm{a}\right)}{\mathrm{x}\:−\:\mathrm{a}}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left({t}+{a}\right)−\mathrm{cos}\:{a}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{t}\mathrm{cos}\:{a}−\mathrm{sin}\:{t}\mathrm{sin}\:{a}−\mathrm{cos}\:{a}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{cos}\:{t}−\mathrm{1}\right)\mathrm{cos}\:{a}−\mathrm{sin}\:{t}\mathrm{sin}\:{a}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{cos}\:{t}−\mathrm{1}\right)\mathrm{cos}\:{a}}{{t}}−\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{t}\mathrm{sin}\:{a}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:^{\mathrm{2}} \frac{{t}}{\mathrm{2}}\mathrm{cos}\:{a}}{{t}^{\mathrm{2}} }×{t}−\:\mathrm{sin}\:{a}\:\:\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{t}}{{t}} \\ $$$$=\mathrm{0}−\mathrm{sin}\:{a} \\ $$$$=−\mathrm{sin}\:{a} \\ $$
Commented by A1B1C1D1 last updated on 27/Jan/18

$$\mathrm{Thanks} \\ $$
Answered by $@ty@m last updated on 27/Jan/18

$${Alternative}: \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\frac{{x}+{a}}{\mathrm{2}}\mathrm{sin}\:\frac{{x}−{a}}{\mathrm{2}}}{{x}−{a}} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\mathrm{sin}\:\frac{{x}+{a}}{\mathrm{2}}\mathrm{sin}\:\frac{{a}−{x}}{\mathrm{2}}}{\frac{{x}−{a}}{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}sin}\:\frac{{x}+{a}}{\mathrm{2}}×\left(−\mathrm{1}×\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\mathrm{sin}\:\frac{{x}−{a}}{\mathrm{2}}}{\frac{{x}−{a}}{\mathrm{2}}}\right) \\ $$$$\mathrm{sin}\:\frac{{a}+{a}}{\mathrm{2}}×\left(−\mathrm{1}\right)×\mathrm{1} \\ $$$$=−\mathrm{sin}\:{a} \\ $$
