let-give-S-n-k-1-n-k-p-p-N-and-n-1-find-the-radius-of-convergence-of-the-serie-n-1-x-n-S-n-

Tinku Tara June 4, 2023 Relation and Functions 0 Comments

Question Number 28531 by abdo imad last updated on 26/Jan/18

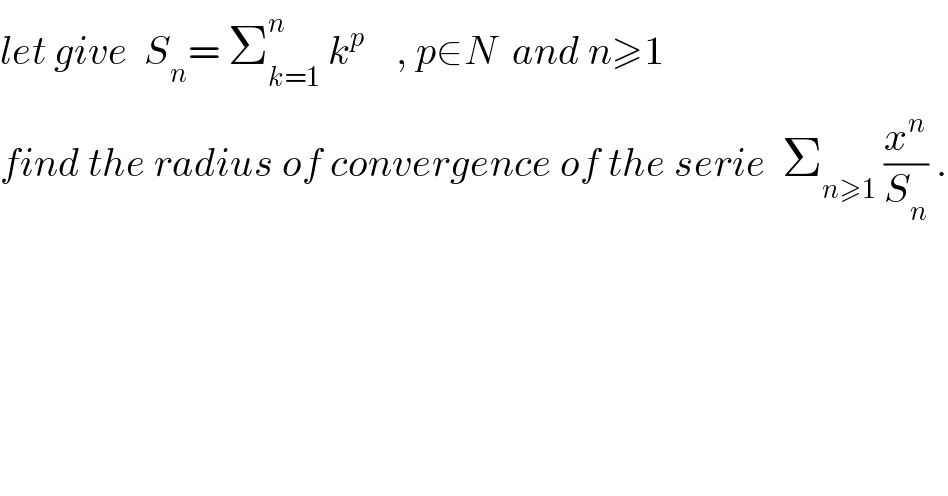
let give S_n = Σ_(k=1) ^n k^p , p∈N and n≥1 find the radius of convergence of the serie Σ_(n≥1) (x^n /S_n ) .

$${let}\:{give}\:\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{{p}} \:\:\:\:,\:{p}\in{N}\:\:{and}\:{n}\geqslant\mathrm{1} \\ $$$${find}\:{the}\:{radius}\:{of}\:{convergence}\:{of}\:{the}\:{serie}\:\:\sum_{{n}\geqslant\mathrm{1}} \:\frac{{x}^{{n}} }{{S}_{{n}} }\:. \\ $$

Facebook Tweet Pin

let-give-S-n-k-1-n-k-p-p-N-and-n-1-find-the-radius-of-convergence-of-the-serie-n-1-x-n-S-n-

Leave a Reply Cancel reply