Question Number 159648 by cortano last updated on 19/Nov/21
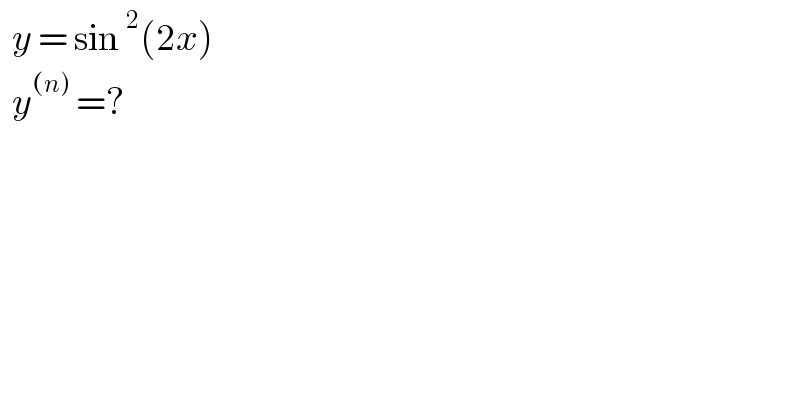
$$\:\:{y}\:=\:\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right) \\ $$$$\:\:{y}^{\left({n}\right)} \:=?\: \\ $$
Answered by FongXD last updated on 19/Nov/21
![• y=(1/2)(1−cos4x)=(1/2)−(1/2)cos4x • y′=2sin4x=−2^(2(1)−1) cos((π/2)+4x) • y′′=8sin((π/2)+4x)=−2^(2(2)−1) cos(((2π)/2)+4x) • y′′′=32sin(((2π)/2)+4x)=−2^(2(3)−1) cos(((3π)/2)+4x) .......................................................... suppose that it′s true all the way up to k-th term: y^((k)) =−2^(2k−1) cos(((kπ)/2)+4x) then y^((k+1)) =[−2^(2k−1) cos(((kπ)/2)+4x)]′ ⇔ y^((k+1)) =2^(2k−1) ×4sin(((kπ)/2)+4x) ⇒ y^((k+1)) =−2^(2(k+1)−1) cos[(((k+1)π)/2)+4x] ✓ therefore, y^((n)) =−2^(2n−1) cos(((nπ)/2)+4x)](https://www.tinkutara.com/question/Q159652.png)
$$\bullet\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos4x}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos4x} \\ $$$$\bullet\:\mathrm{y}'=\mathrm{2sin4x}=−\mathrm{2}^{\mathrm{2}\left(\mathrm{1}\right)−\mathrm{1}} \mathrm{cos}\left(\frac{\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$$$\bullet\:\mathrm{y}''=\mathrm{8sin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{4x}\right)=−\mathrm{2}^{\mathrm{2}\left(\mathrm{2}\right)−\mathrm{1}} \mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$$$\bullet\:\mathrm{y}'''=\mathrm{32sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2}}+\mathrm{4x}\right)=−\mathrm{2}^{\mathrm{2}\left(\mathrm{3}\right)−\mathrm{1}} \mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$$$…………………………………………………. \\ $$$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{all}\:\mathrm{the}\:\mathrm{way}\:\mathrm{up}\:\mathrm{to}\:\mathrm{k}-\mathrm{th}\:\mathrm{term}:\:\mathrm{y}^{\left(\mathrm{k}\right)} =−\mathrm{2}^{\mathrm{2k}−\mathrm{1}} \mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$$$\mathrm{then}\:\mathrm{y}^{\left(\mathrm{k}+\mathrm{1}\right)} =\left[−\mathrm{2}^{\mathrm{2k}−\mathrm{1}} \mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{2}}+\mathrm{4x}\right)\right]' \\ $$$$\Leftrightarrow\:\mathrm{y}^{\left(\mathrm{k}+\mathrm{1}\right)} =\mathrm{2}^{\mathrm{2k}−\mathrm{1}} ×\mathrm{4sin}\left(\frac{\mathrm{k}\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$$$\Rightarrow\:\mathrm{y}^{\left(\mathrm{k}+\mathrm{1}\right)} =−\mathrm{2}^{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)−\mathrm{1}} \mathrm{cos}\left[\frac{\left(\mathrm{k}+\mathrm{1}\right)\pi}{\mathrm{2}}+\mathrm{4x}\right]\:\:\:\checkmark \\ $$$$\mathrm{therefore},\:\mathrm{y}^{\left(\mathrm{n}\right)} =−\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}+\mathrm{4x}\right) \\ $$
Commented by bobhans last updated on 19/Nov/21
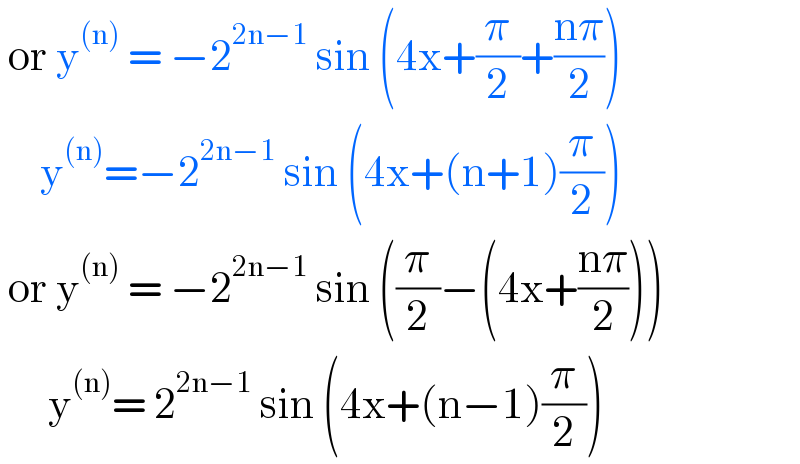
$$\:\mathrm{or}\:\mathrm{y}^{\left(\mathrm{n}\right)} \:=\:−\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \:\mathrm{sin}\:\left(\mathrm{4x}+\frac{\pi}{\mathrm{2}}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\mathrm{y}^{\left(\mathrm{n}\right)} =−\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \:\mathrm{sin}\:\left(\mathrm{4x}+\left(\mathrm{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:\mathrm{or}\:\mathrm{y}^{\left(\mathrm{n}\right)} \:=\:−\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\left(\mathrm{4x}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\mathrm{y}^{\left(\mathrm{n}\right)} =\:\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \:\mathrm{sin}\:\left(\mathrm{4x}+\left(\mathrm{n}−\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\right) \\ $$
Answered by mathmax by abdo last updated on 20/Nov/21
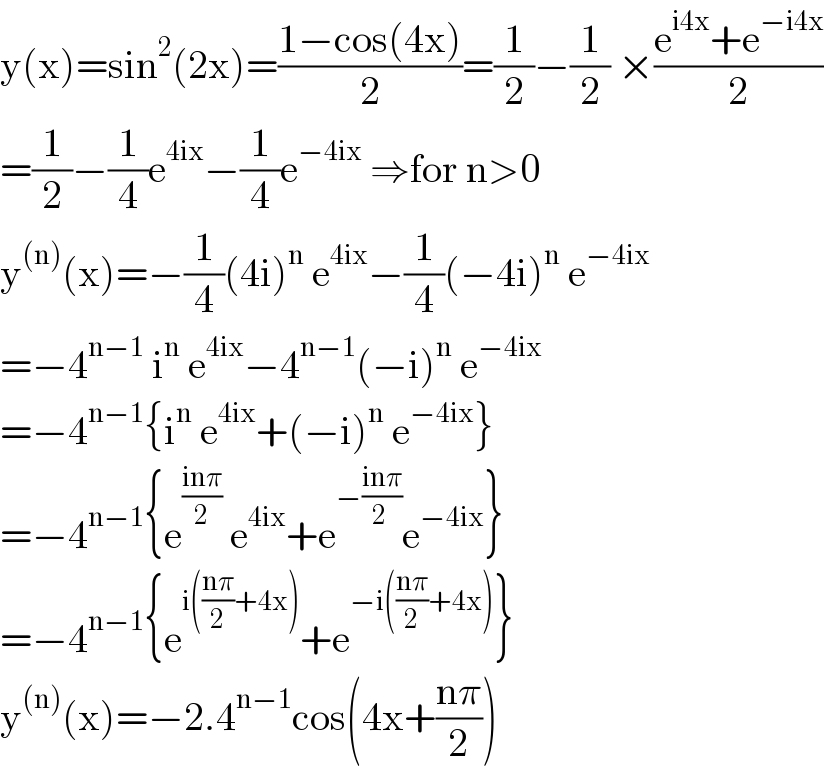
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:×\frac{\mathrm{e}^{\mathrm{i4x}} +\mathrm{e}^{−\mathrm{i4x}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{4ix}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{4ix}} \:\Rightarrow\mathrm{for}\:\mathrm{n}>\mathrm{0} \\ $$$$\mathrm{y}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4i}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{4ix}} −\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{4i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{4ix}} \\ $$$$=−\mathrm{4}^{\mathrm{n}−\mathrm{1}} \:\mathrm{i}^{\mathrm{n}} \:\mathrm{e}^{\mathrm{4ix}} −\mathrm{4}^{\mathrm{n}−\mathrm{1}} \left(−\mathrm{i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{4ix}} \\ $$$$=−\mathrm{4}^{\mathrm{n}−\mathrm{1}} \left\{\mathrm{i}^{\mathrm{n}} \:\mathrm{e}^{\mathrm{4ix}} +\left(−\mathrm{i}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{4ix}} \right\} \\ $$$$=−\mathrm{4}^{\mathrm{n}−\mathrm{1}} \left\{\mathrm{e}^{\frac{\mathrm{in}\pi}{\mathrm{2}}} \:\mathrm{e}^{\mathrm{4ix}} +\mathrm{e}^{−\frac{\mathrm{in}\pi}{\mathrm{2}\:}} \mathrm{e}^{−\mathrm{4ix}} \right\} \\ $$$$=−\mathrm{4}^{\mathrm{n}−\mathrm{1}} \left\{\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}+\mathrm{4x}\right)} +\mathrm{e}^{−\mathrm{i}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}+\mathrm{4x}\right)} \right\} \\ $$$$\mathrm{y}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=−\mathrm{2}.\mathrm{4}^{\mathrm{n}−\mathrm{1}} \mathrm{cos}\left(\mathrm{4x}+\frac{\mathrm{n}\pi}{\mathrm{2}}\right) \\ $$
