Question Number 28770 by Rasheed.Sindhi last updated on 30/Jan/18
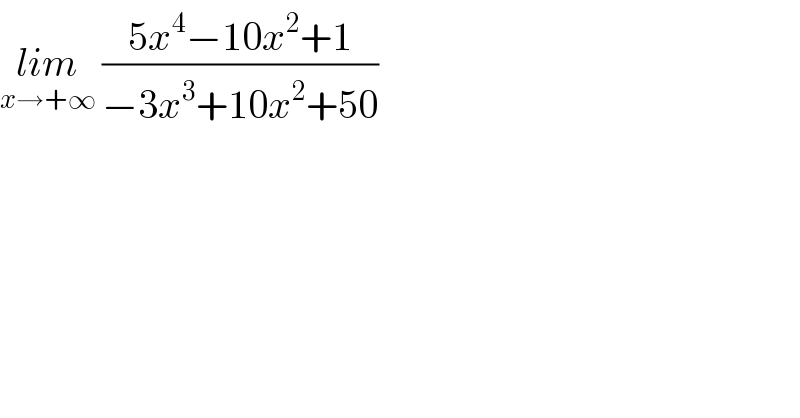
$$\underset{{x}\rightarrow+\infty} {{lim}}\:\frac{\mathrm{5}{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{1}}{−\mathrm{3}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{50}} \\ $$
Commented by Cheyboy last updated on 30/Jan/18

$$\underset{{x}\rightarrow+\infty\:} {\mathrm{lim}}\:\:\:\frac{\frac{\mathrm{5}{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} }\:−\:\frac{\mathrm{10}{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} }\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:}{\frac{−\mathrm{3}{x}^{\mathrm{3}} }{{x}^{\mathrm{4}} }\:−\:\frac{\mathrm{10}{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} }\:−\:\frac{\mathrm{50}}{{x}^{\mathrm{4}} }} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{5}−\mathrm{0}−\mathrm{0}}{\mathrm{0}−\mathrm{0}−\mathrm{0}}=\mathrm{5} \\ $$$${i}\:{even}\:{forget}\:{that}\:\frac{\mathrm{5}}{\mathrm{0}}=\infty \\ $$$${so}\:{my}\:{answer}\:{seems}\:{correct} \\ $$
Commented by abdo imad last updated on 30/Jan/18
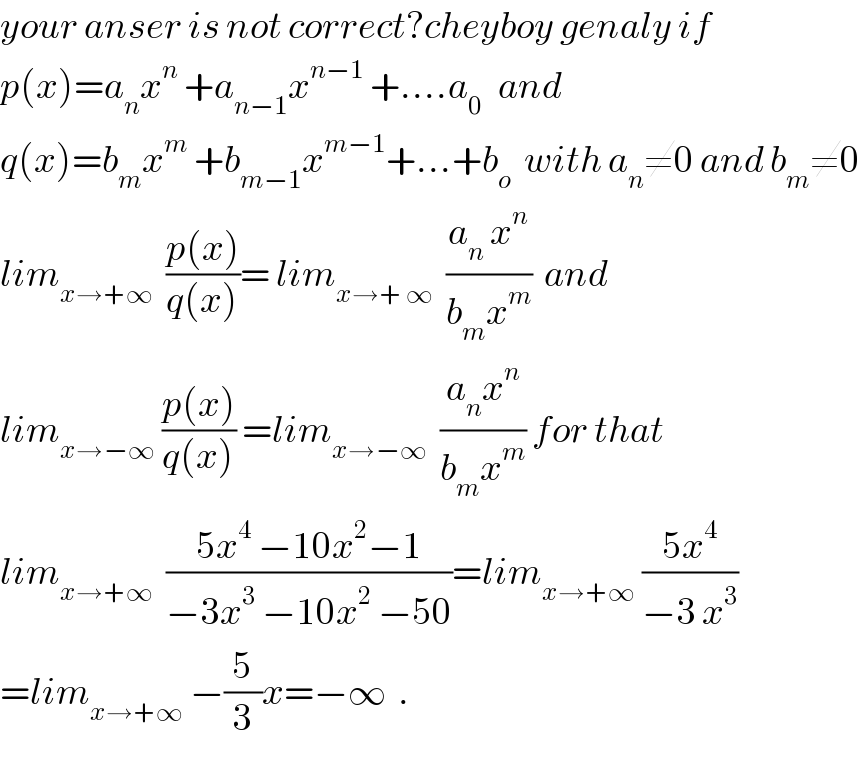
$${your}\:{anser}\:{is}\:{not}\:{correct}?{cheyboy}\:{genaly}\:{if} \\ $$$${p}\left({x}\right)={a}_{{n}} {x}^{{n}} \:+{a}_{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} \:+….{a}_{\mathrm{0}\:} \:\:{and} \\ $$$${q}\left({x}\right)={b}_{{m}} {x}^{{m}} \:+{b}_{{m}−\mathrm{1}} {x}^{{m}−\mathrm{1}} +…+{b}_{{o}} \:\:{with}\:{a}_{{n}} \neq\mathrm{0}\:{and}\:{b}_{{m}} \neq\mathrm{0} \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}=\:{lim}_{{x}\rightarrow+\:\infty} \:\:\frac{{a}_{{n}} \:{x}^{{n}} }{{b}_{{m}} {x}^{{m}} }\:\:{and} \\ $$$${lim}_{{x}\rightarrow−\infty} \:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}\:={lim}_{{x}\rightarrow−\infty} \:\:\frac{{a}_{{n}} {x}^{{n}} }{{b}_{{m}} {x}^{{m}} }\:{for}\:{that} \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:\frac{\mathrm{5}{x}^{\mathrm{4}} \:−\mathrm{10}{x}^{\mathrm{2}} −\mathrm{1}}{−\mathrm{3}{x}^{\mathrm{3}} \:−\mathrm{10}{x}^{\mathrm{2}} \:−\mathrm{50}}={lim}_{{x}\rightarrow+\infty} \:\frac{\mathrm{5}{x}^{\mathrm{4}} }{−\mathrm{3}\:{x}^{\mathrm{3}} } \\ $$$$={lim}_{{x}\rightarrow+\infty} \:−\frac{\mathrm{5}}{\mathrm{3}}{x}=−\infty\:\:. \\ $$
Commented by abdo imad last updated on 30/Jan/18
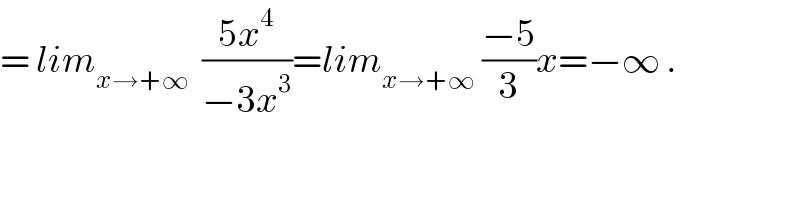
$$=\:{lim}_{{x}\rightarrow+\infty} \:\:\frac{\mathrm{5}{x}^{\mathrm{4}} }{−\mathrm{3}{x}^{\mathrm{3}} }={lim}_{{x}\rightarrow+\infty} \:\frac{−\mathrm{5}}{\mathrm{3}}{x}=−\infty\:. \\ $$
Commented by Cheyboy last updated on 30/Jan/18

$${Thank}\:{sir}\:{for}\:{the}\:{rectification} \\ $$$$ \\ $$$$ \\ $$
Commented by Cheyboy last updated on 30/Jan/18

$${Thank}\:{sir}\:{for}\:{the}\:{rectification} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jan/18

$$\mathcal{T}{hank}\:{you}\:{both}! \\ $$
Answered by ajfour last updated on 30/Jan/18
![=lim_(x→+∞) x[((5x^3 −10x−(1/x))/(−3x^3 +10x^2 +50))] =(lim_(x→+∞) x)×lim_(x→+∞) (((5−((10)/x^2 )−(1/x^3 ))/(−3+((10)/x)+((50)/x^3 )))) = −(5/3)lim_(x→+∞) (x) = −∞ .](https://www.tinkutara.com/question/Q28778.png)
$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{x}\left[\frac{\mathrm{5}{x}^{\mathrm{3}} −\mathrm{10}{x}−\frac{\mathrm{1}}{{x}}}{−\mathrm{3}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{50}}\right] \\ $$$$\:\:=\left(\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{x}\right)×\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{5}−\frac{\mathrm{10}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}{−\mathrm{3}+\frac{\mathrm{10}}{{x}}+\frac{\mathrm{50}}{{x}^{\mathrm{3}} }}\right) \\ $$$$=\:−\frac{\mathrm{5}}{\mathrm{3}}\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left({x}\right)\:=\:−\infty\:. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jan/18

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jan/18
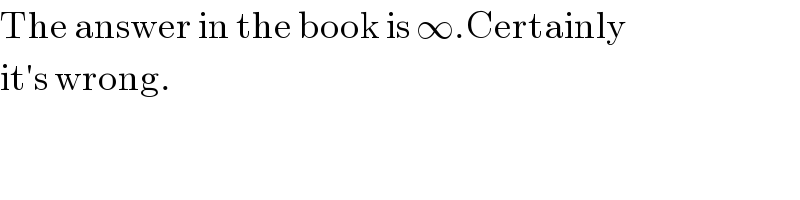
$$\mathrm{The}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{the}\:\mathrm{book}\:\mathrm{is}\:\infty.\mathrm{Certainly} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{wrong}. \\ $$
