Question Number 133708 by Dwaipayan Shikari last updated on 23/Feb/21
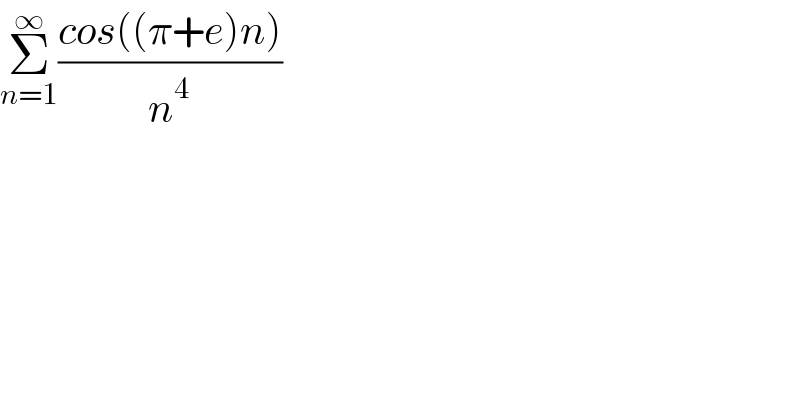
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left(\left(\pi+{e}\right){n}\right)}{{n}^{\mathrm{4}} } \\ $$
Answered by mindispower last updated on 24/Feb/21
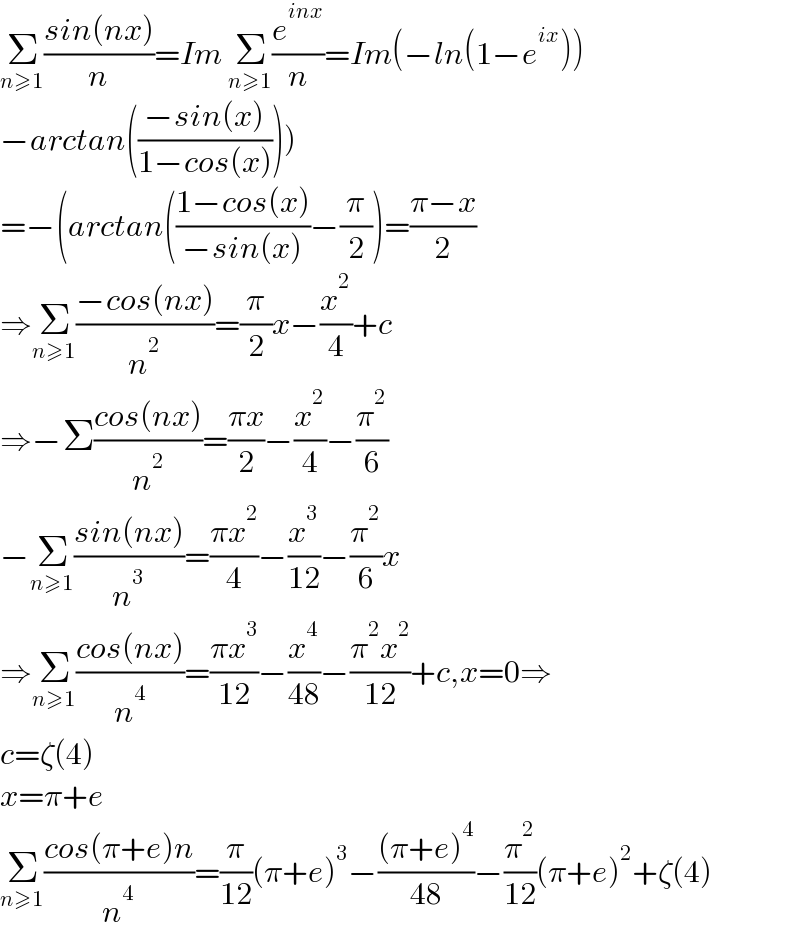
$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({nx}\right)}{{n}}={Im}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{e}^{{inx}} }{{n}}={Im}\left(−{ln}\left(\mathrm{1}−{e}^{{ix}} \right)\right) \\ $$$$\left.−{arctan}\left(\frac{−{sin}\left({x}\right)}{\mathrm{1}−{cos}\left({x}\right)}\right)\right) \\ $$$$=−\left({arctan}\left(\frac{\mathrm{1}−{cos}\left({x}\right)}{−{sin}\left({x}\right)}−\frac{\pi}{\mathrm{2}}\right)=\frac{\pi−{x}}{\mathrm{2}}\right. \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{−{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{c} \\ $$$$\Rightarrow−\Sigma\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }=\frac{\pi{x}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{12}}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{x} \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{4}} }=\frac{\pi{x}^{\mathrm{3}} }{\mathrm{12}}−\frac{{x}^{\mathrm{4}} }{\mathrm{48}}−\frac{\pi^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{12}}+{c},{x}=\mathrm{0}\Rightarrow \\ $$$${c}=\zeta\left(\mathrm{4}\right) \\ $$$${x}=\pi+{e} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\pi+{e}\right){n}}{{n}^{\mathrm{4}} }=\frac{\pi}{\mathrm{12}}\left(\pi+{e}\right)^{\mathrm{3}} −\frac{\left(\pi+{e}\right)^{\mathrm{4}} }{\mathrm{48}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\left(\pi+{e}\right)^{\mathrm{2}} +\zeta\left(\mathrm{4}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 24/Feb/21
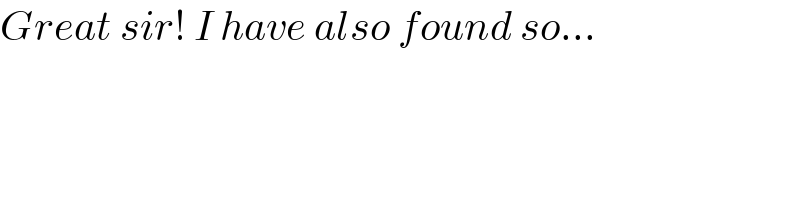
$${Great}\:{sir}!\:{I}\:{have}\:{also}\:{found}\:{so}… \\ $$
