Question Number 28890 by abdo imad last updated on 31/Jan/18
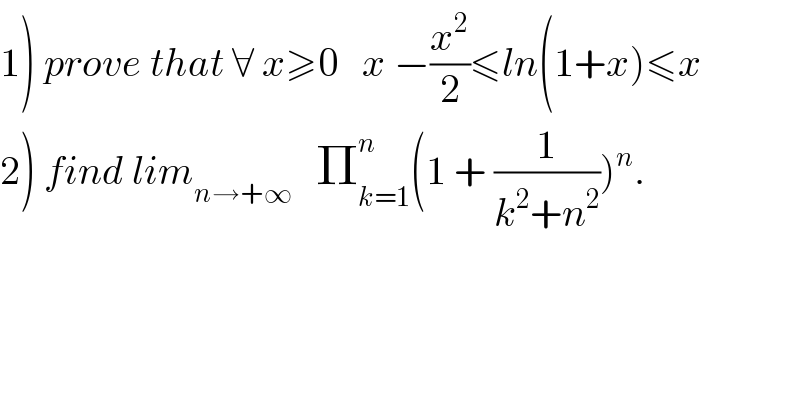
$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\forall\:{x}\geqslant\mathrm{0}\:\:\:{x}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{n}^{\mathrm{2}} }\right)^{{n}} . \\ $$
