Menu Close

find-k-n-1-n-k-n-with-k-1-

Tinku Tara 0 Comments
Pin




Question Number 160052 by mr W last updated on 24/Nov/21
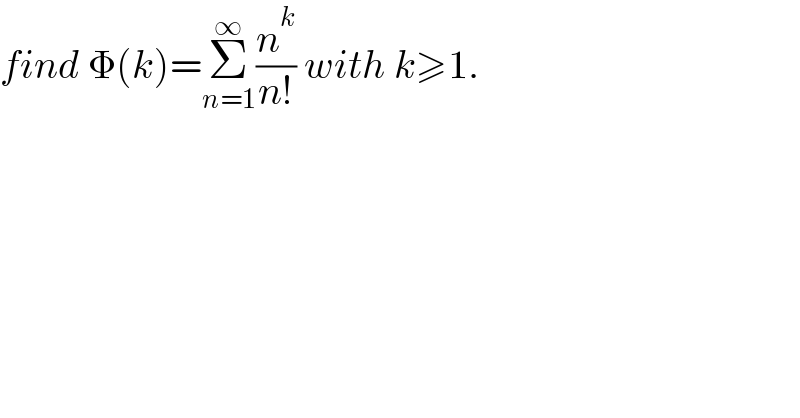
find Φ(k)=Σ_(n=1) ^∞ (n^k /(n!)) with k≥1.
$${find}\:\Phi\left({k}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{k}} }{{n}!}\:{with}\:{k}\geqslant\mathrm{1}. \\ $$
Answered by Tokugami last updated on 24/Nov/21
Σ_(n=0) ^∞ (1/(n!))=e Φ(k)=Σ_(n=1) ^∞ (n^k /(n!)) =Σ_(n=1) ^∞ (n^(k−1) /((n−1)!))=^(n−1→n) Σ_(n=0) ^∞ (((n+1)^(k−1) )/(n!)) (n+1)^(k−1) = (((k−1)),(0) ) n^0 + (((k−1)),(1) ) n^1 + (((k−1)),(2) ) n^2 +...+ (((k−1)),((k−2)) ) n^(k−2) + (((k−1)),((k−1)) ) n^(k−1) =Σ_(i=0) ^(k−1) (((k−1)),(i) ) n^i Φ(k)=Σ_(n=0) ^∞ ((1/(n!))Σ_(i=0) ^(k−1) (((k−1)),(i) ) n^i ) =Σ_(n=0) ^∞ (Σ_(i=0) ^(k−1) (((k−1)),(i) ) (n^i /(n!))) Φ(4)=Σ_(i=0) ^3 ((3),(i) )(Σ_(n=0) ^∞ (n^i /(n!))) Φ(k)=e+Σ_(i=1) ^(k−1) ( (((k−1)),(i) ) Φ(i)) I think this is correct?
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!}={e} \\ $$$$\Phi\left({k}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{k}} }{{n}!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{k}−\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}\overset{{n}−\mathrm{1}\rightarrow{n}} {=}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)^{{k}−\mathrm{1}} }{{n}!} \\ $$$$ \\ $$$$\left({n}+\mathrm{1}\right)^{{k}−\mathrm{1}} =\begin{pmatrix}{{k}−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:{n}^{\mathrm{0}} +\begin{pmatrix}{{k}−\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}\:{n}^{\mathrm{1}} +\begin{pmatrix}{{k}−\mathrm{1}}\\{\mathrm{2}}\end{pmatrix}\:{n}^{\mathrm{2}} +…+\begin{pmatrix}{{k}−\mathrm{1}}\\{{k}−\mathrm{2}}\end{pmatrix}\:{n}^{{k}−\mathrm{2}} +\begin{pmatrix}{{k}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{n}^{{k}−\mathrm{1}} \\ $$$$=\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\begin{pmatrix}{{k}−\mathrm{1}}\\{{i}}\end{pmatrix}\:{n}^{{i}} \\ $$$$\Phi\left({k}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}!}\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\begin{pmatrix}{{k}−\mathrm{1}}\\{{i}}\end{pmatrix}\:{n}^{{i}} \right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\begin{pmatrix}{{k}−\mathrm{1}}\\{{i}}\end{pmatrix}\:\frac{{n}^{{i}} }{{n}!}\right) \\ $$$$\Phi\left(\mathrm{4}\right)=\underset{{i}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\begin{pmatrix}{\mathrm{3}}\\{{i}}\end{pmatrix}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}^{{i}} }{{n}!}\right) \\ $$$$\Phi\left({k}\right)={e}+\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\sum}}\left(\begin{pmatrix}{{k}−\mathrm{1}}\\{{i}}\end{pmatrix}\:\Phi\left({i}\right)\right) \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{correct}? \\ $$$$ \\ $$
Commented by mr W last updated on 25/Nov/21
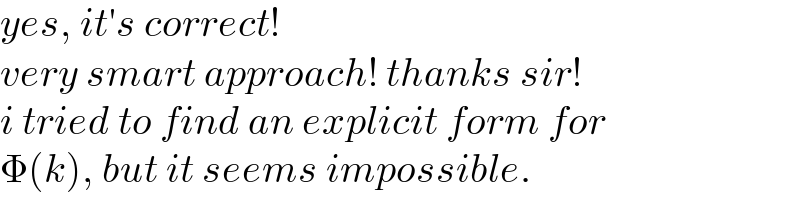
yes, it′s correct! very smart approach! thanks sir! i tried to find an explicit form for Φ(k), but it seems impossible.
$${yes},\:{it}'{s}\:{correct}! \\ $$$${very}\:{smart}\:{approach}!\:{thanks}\:{sir}! \\ $$$${i}\:{tried}\:{to}\:{find}\:{an}\:{explicit}\:{form}\:{for}\: \\ $$$$\Phi\left({k}\right),\:{but}\:{it}\:{seems}\:{impossible}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *