Question-133730

Question Number 133730 by mr W last updated on 24/Feb/21

Commented by mr W last updated on 23/Feb/21

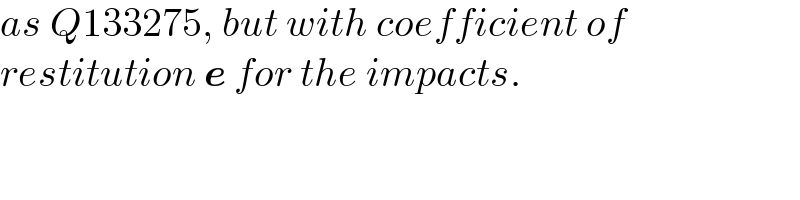
as Q133275, but with coefficient of restitution e for the impacts.

$${as}\:{Q}\mathrm{133275},\:{but}\:{with}\:{coefficient}\:{of} \\ $$$${restitution}\:\boldsymbol{{e}}\:{for}\:{the}\:{impacts}. \\ $$

Commented by Abdoulaye last updated on 23/Feb/21

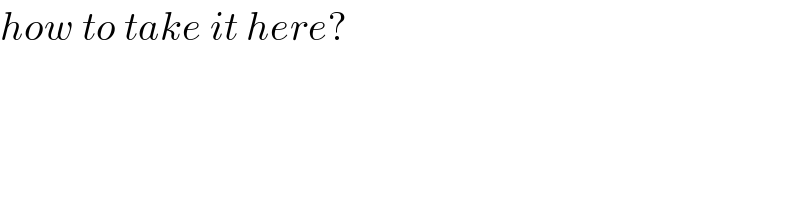
$${how}\:{to}\:{take}\:{it}\:{here}? \\ $$

Answered by mr W last updated on 23/Feb/21

Commented by mr W last updated on 26/Feb/21

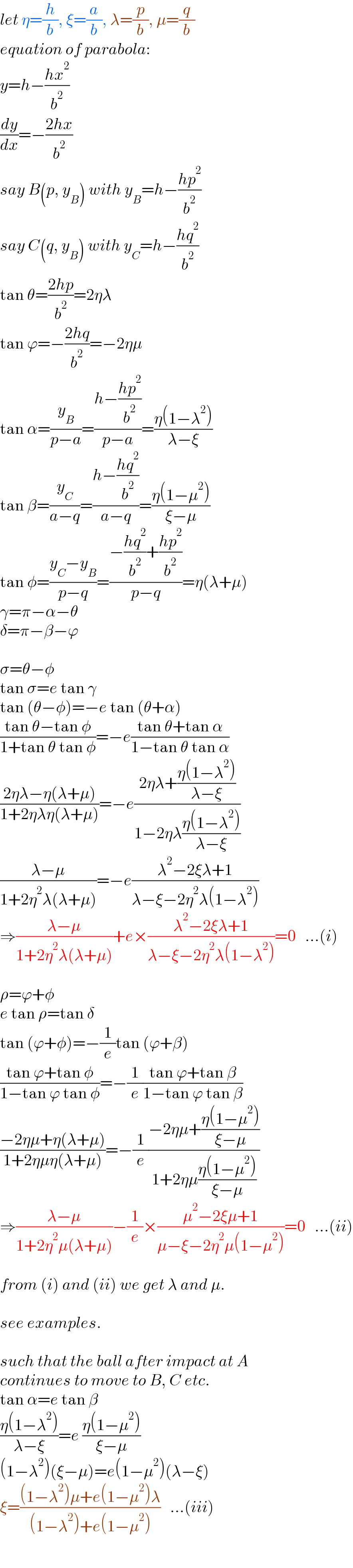
let η=(h/b), ξ=(a/b), λ=(p/b), μ=(q/b) equation of parabola: y=h−((hx^2 )/b^2 ) (dy/dx)=−((2hx)/b^2 ) say B(p, y_B ) with y_B =h−((hp^2 )/b^2 ) say C(q, y_B ) with y_C =h−((hq^2 )/b^2 ) tan θ=((2hp)/b^2 )=2ηλ tan ϕ=−((2hq)/b^2 )=−2ημ tan α=(y_B /(p−a))=((h−((hp^2 )/b^2 ))/(p−a))=((η(1−λ^2 ))/(λ−ξ)) tan β=(y_C /(a−q))=((h−((hq^2 )/b^2 ))/(a−q))=((η(1−μ^2 ))/(ξ−μ)) tan φ=((y_C −y_B )/(p−q))=((−((hq^2 )/b^2 )+((hp^2 )/b^2 ))/(p−q))=η(λ+μ) γ=π−α−θ δ=π−β−ϕ σ=θ−φ tan σ=e tan γ tan (θ−φ)=−e tan (θ+α) ((tan θ−tan φ)/(1+tan θ tan φ))=−e((tan θ+tan α)/(1−tan θ tan α)) ((2ηλ−η(λ+μ))/(1+2ηλη(λ+μ)))=−e((2ηλ+((η(1−λ^2 ))/(λ−ξ)))/(1−2ηλ((η(1−λ^2 ))/(λ−ξ)))) ((λ−μ)/(1+2η^2 λ(λ+μ)))=−e((λ^2 −2ξλ+1)/(λ−ξ−2η^2 λ(1−λ^2 ))) ⇒((λ−μ)/(1+2η^2 λ(λ+μ)))+e×((λ^2 −2ξλ+1)/(λ−ξ−2η^2 λ(1−λ^2 )))=0 ...(i) ρ=ϕ+φ e tan ρ=tan δ tan (ϕ+φ)=−(1/e)tan (ϕ+β) ((tan ϕ+tan φ)/(1−tan ϕ tan φ))=−(1/e)((tan ϕ+tan β)/(1−tan ϕ tan β)) ((−2ημ+η(λ+μ))/(1+2ημη(λ+μ)))=−(1/e)((−2ημ+((η(1−μ^2 ))/(ξ−μ)))/(1+2ημ((η(1−μ^2 ))/(ξ−μ)))) ⇒((λ−μ)/(1+2η^2 μ(λ+μ)))−(1/e)×((μ^2 −2ξμ+1)/(μ−ξ−2η^2 μ(1−μ^2 )))=0 ...(ii) from (i) and (ii) we get λ and μ. see examples. such that the ball after impact at A continues to move to B, C etc. tan α=e tan β ((η(1−λ^2 ))/(λ−ξ))=e ((η(1−μ^2 ))/(ξ−μ)) (1−λ^2 )(ξ−μ)=e(1−μ^2 )(λ−ξ) ξ=(((1−λ^2 )μ+e(1−μ^2 )λ)/((1−λ^2 )+e(1−μ^2 ))) ...(iii)

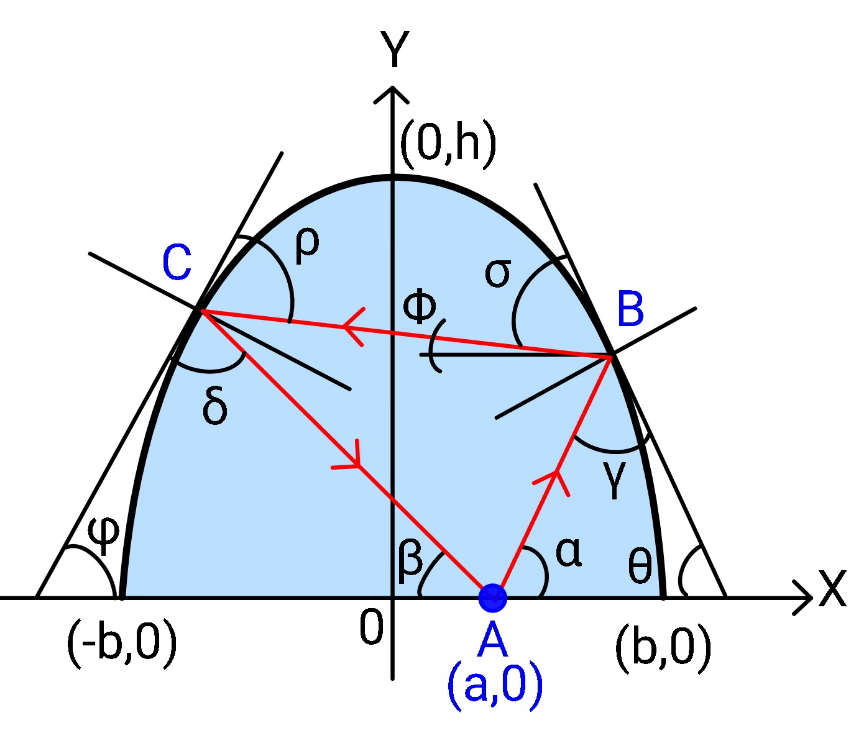
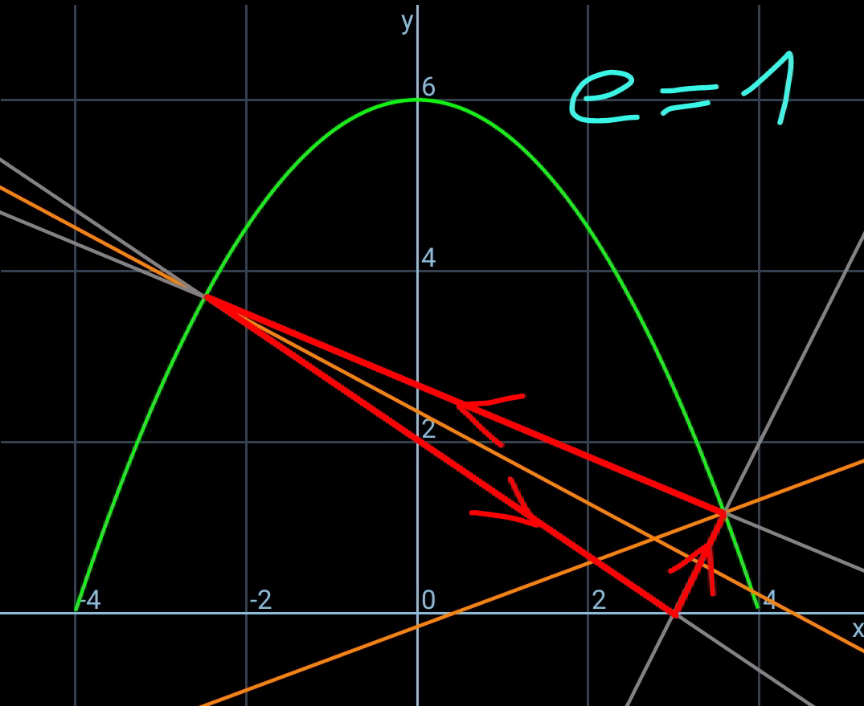
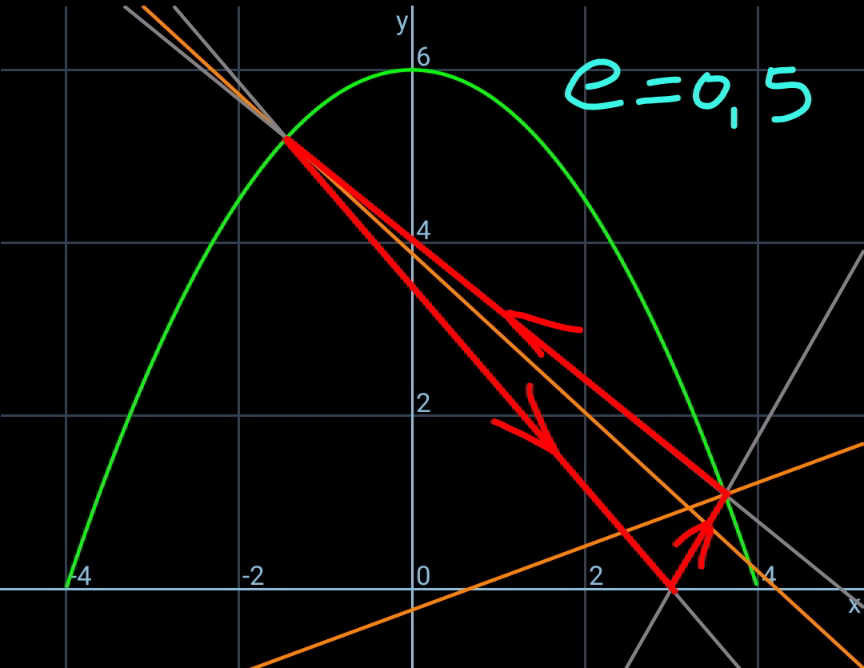
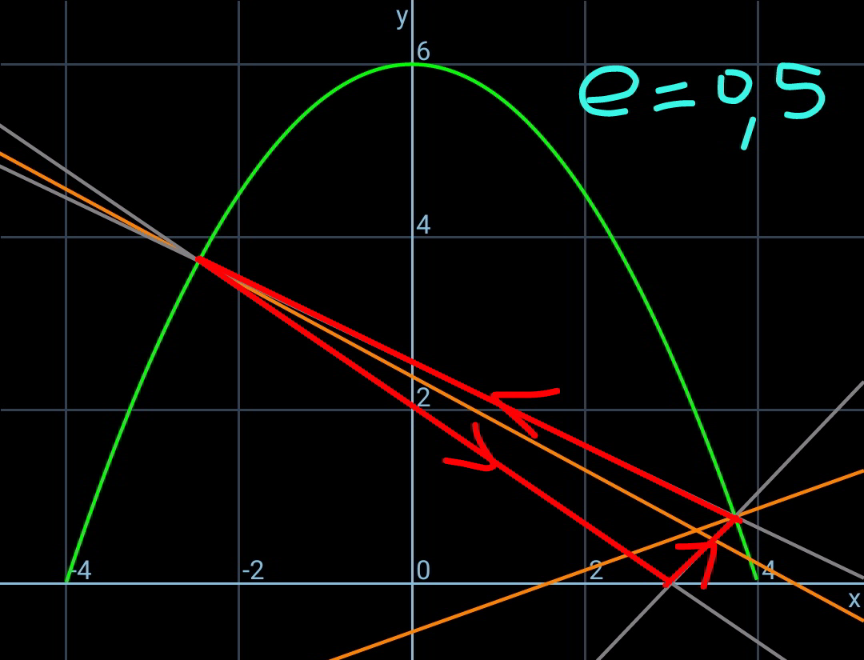
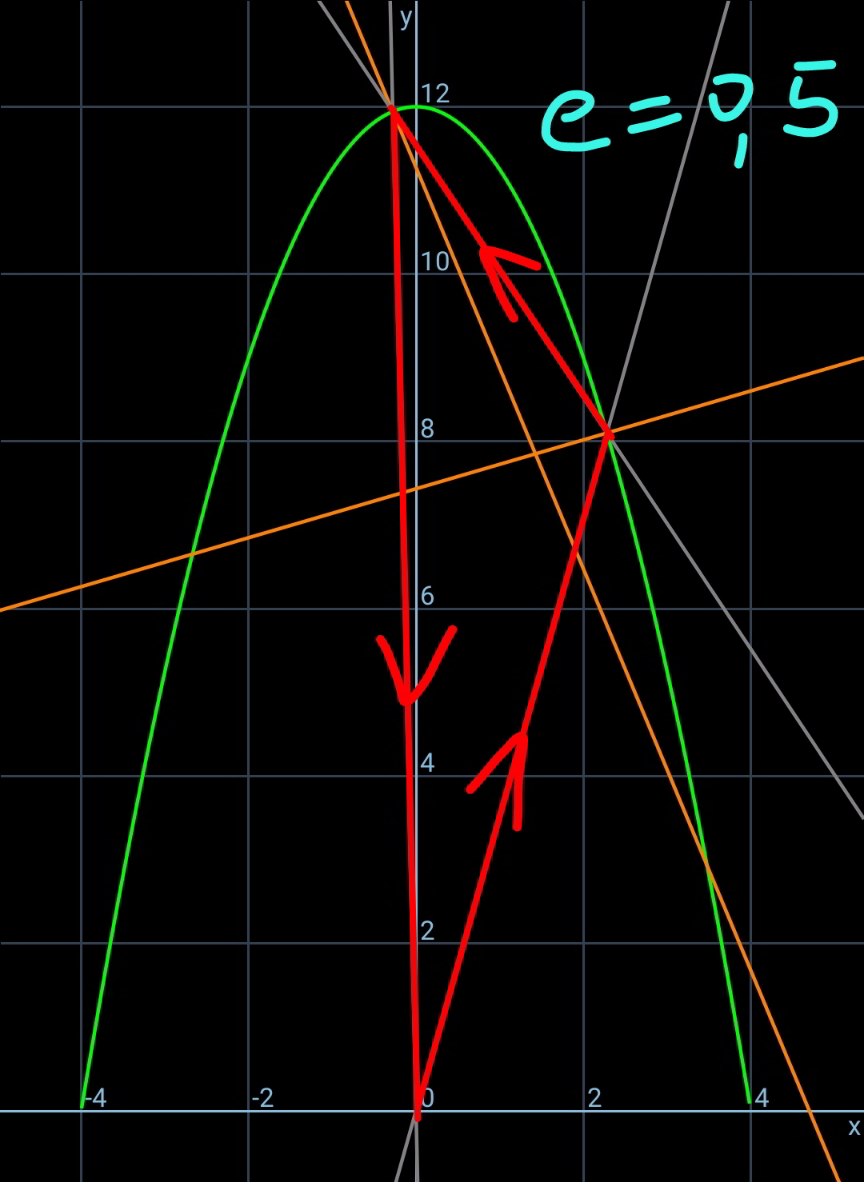
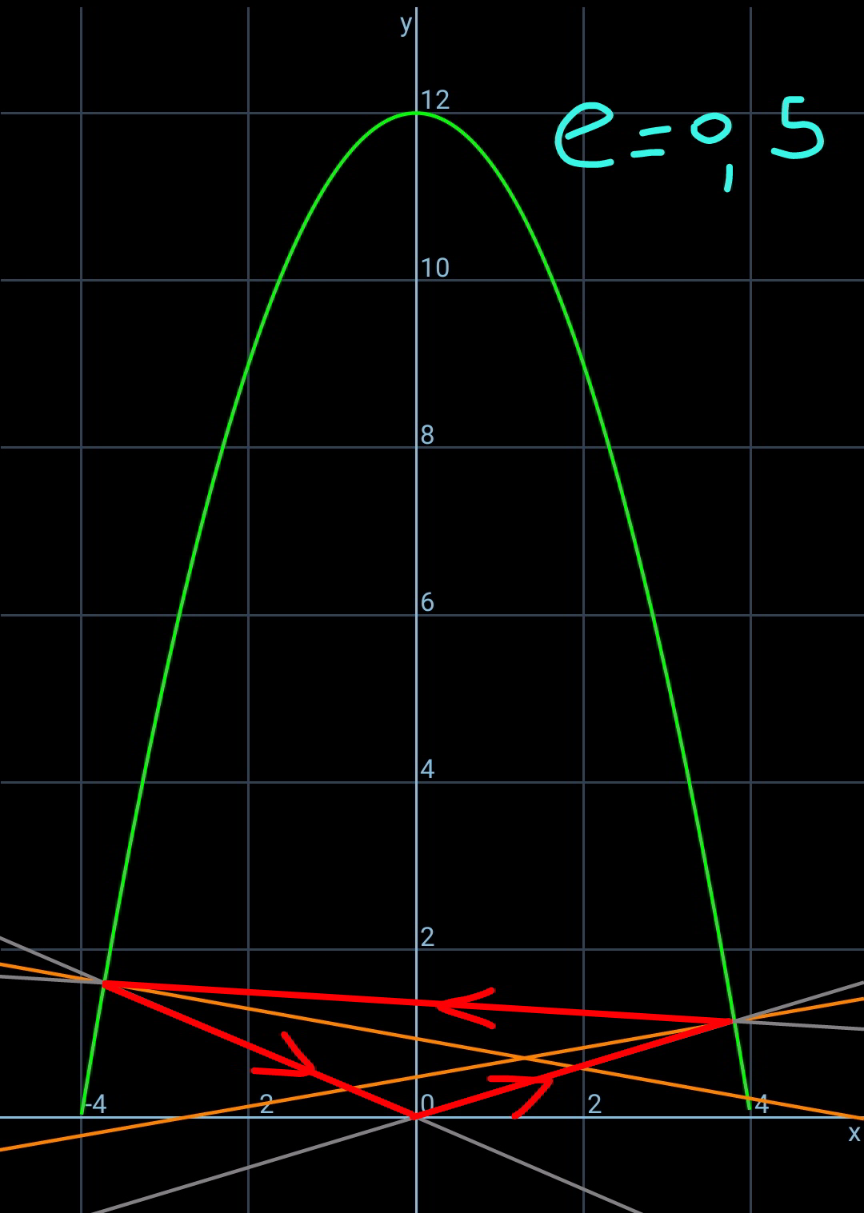
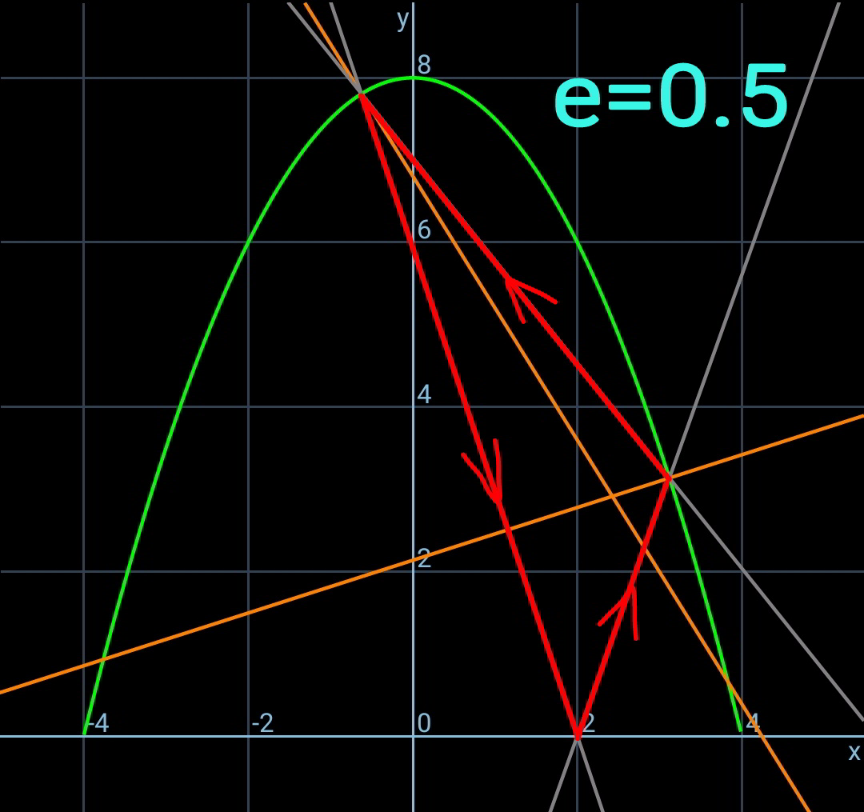
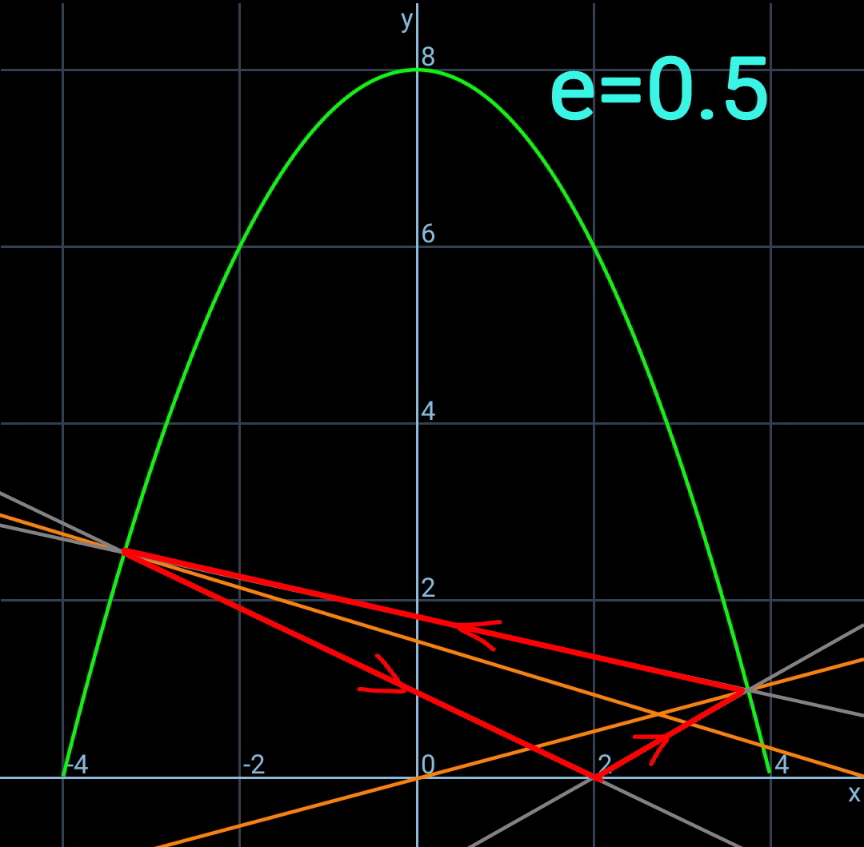
$${let}\:\eta=\frac{{h}}{{b}},\:\xi=\frac{{a}}{{b}},\:\lambda=\frac{{p}}{{b}},\:\mu=\frac{{q}}{{b}} \\ $$$${equation}\:{of}\:{parabola}: \\ $$$${y}={h}−\frac{{hx}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{2}{hx}}{{b}^{\mathrm{2}} } \\ $$$${say}\:{B}\left({p},\:{y}_{{B}} \right)\:{with}\:{y}_{{B}} ={h}−\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${say}\:{C}\left({q},\:{y}_{{B}} \right)\:{with}\:{y}_{{C}} ={h}−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}{hp}}{{b}^{\mathrm{2}} }=\mathrm{2}\eta\lambda \\ $$$$\mathrm{tan}\:\varphi=−\frac{\mathrm{2}{hq}}{{b}^{\mathrm{2}} }=−\mathrm{2}\eta\mu \\ $$$$\mathrm{tan}\:\alpha=\frac{{y}_{{B}} }{{p}−{a}}=\frac{{h}−\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{p}−{a}}=\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi} \\ $$$$\mathrm{tan}\:\beta=\frac{{y}_{{C}} }{{a}−{q}}=\frac{{h}−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{a}−{q}}=\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu} \\ $$$$\mathrm{tan}\:\phi=\frac{{y}_{{C}} −{y}_{{B}} }{{p}−{q}}=\frac{−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{p}−{q}}=\eta\left(\lambda+\mu\right) \\ $$$$\gamma=\pi−\alpha−\theta \\ $$$$\delta=\pi−\beta−\varphi \\ $$$$ \\ $$$$\sigma=\theta−\phi \\ $$$$\mathrm{tan}\:\sigma={e}\:\mathrm{tan}\:\gamma \\ $$$$\mathrm{tan}\:\left(\theta−\phi\right)=−{e}\:\mathrm{tan}\:\left(\theta+\alpha\right) \\ $$$$\frac{\mathrm{tan}\:\theta−\mathrm{tan}\:\phi}{\mathrm{1}+\mathrm{tan}\:\theta\:\mathrm{tan}\:\phi}=−{e}\frac{\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:\theta\:\mathrm{tan}\:\alpha} \\ $$$$\frac{\mathrm{2}\eta\lambda−\eta\left(\lambda+\mu\right)}{\mathrm{1}+\mathrm{2}\eta\lambda\eta\left(\lambda+\mu\right)}=−{e}\frac{\mathrm{2}\eta\lambda+\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi}}{\mathrm{1}−\mathrm{2}\eta\lambda\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi}} \\ $$$$\frac{\lambda−\mu}{\mathrm{1}+\mathrm{2}\eta^{\mathrm{2}} \lambda\left(\lambda+\mu\right)}=−{e}\frac{\lambda^{\mathrm{2}} −\mathrm{2}\xi\lambda+\mathrm{1}}{\lambda−\xi−\mathrm{2}\eta^{\mathrm{2}} \lambda\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\frac{\lambda−\mu}{\mathrm{1}+\mathrm{2}\eta^{\mathrm{2}} \lambda\left(\lambda+\mu\right)}+{e}×\frac{\lambda^{\mathrm{2}} −\mathrm{2}\xi\lambda+\mathrm{1}}{\lambda−\xi−\mathrm{2}\eta^{\mathrm{2}} \lambda\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\rho=\varphi+\phi \\ $$$${e}\:\mathrm{tan}\:\rho=\mathrm{tan}\:\delta \\ $$$$\mathrm{tan}\:\left(\varphi+\phi\right)=−\frac{\mathrm{1}}{{e}}\mathrm{tan}\:\left(\varphi+\beta\right) \\ $$$$\frac{\mathrm{tan}\:\varphi+\mathrm{tan}\:\phi}{\mathrm{1}−\mathrm{tan}\:\varphi\:\mathrm{tan}\:\phi}=−\frac{\mathrm{1}}{{e}}\frac{\mathrm{tan}\:\varphi+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\varphi\:\mathrm{tan}\:\beta} \\ $$$$\frac{−\mathrm{2}\eta\mu+\eta\left(\lambda+\mu\right)}{\mathrm{1}+\mathrm{2}\eta\mu\eta\left(\lambda+\mu\right)}=−\frac{\mathrm{1}}{{e}}\frac{−\mathrm{2}\eta\mu+\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu}}{\mathrm{1}+\mathrm{2}\eta\mu\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu}} \\ $$$$\Rightarrow\frac{\lambda−\mu}{\mathrm{1}+\mathrm{2}\eta^{\mathrm{2}} \mu\left(\lambda+\mu\right)}−\frac{\mathrm{1}}{{e}}×\frac{\mu^{\mathrm{2}} −\mathrm{2}\xi\mu+\mathrm{1}}{\mu−\xi−\mathrm{2}\eta^{\mathrm{2}} \mu\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}\:\lambda\:{and}\:\mu. \\ $$$$ \\ $$$${see}\:{examples}. \\ $$$$ \\ $$$${such}\:{that}\:{the}\:{ball}\:{after}\:{impact}\:{at}\:{A} \\ $$$${continues}\:{to}\:{move}\:{to}\:{B},\:{C}\:{etc}. \\ $$$$\mathrm{tan}\:\alpha={e}\:\mathrm{tan}\:\beta \\ $$$$\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi}={e}\:\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu} \\ $$$$\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\left(\xi−\mu\right)={e}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\lambda−\xi\right) \\ $$$$\xi=\frac{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\mu+{e}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\lambda}{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)+{e}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}\:\:\:…\left({iii}\right) \\ $$