Question Number 29116 by tawa tawa last updated on 04/Feb/18
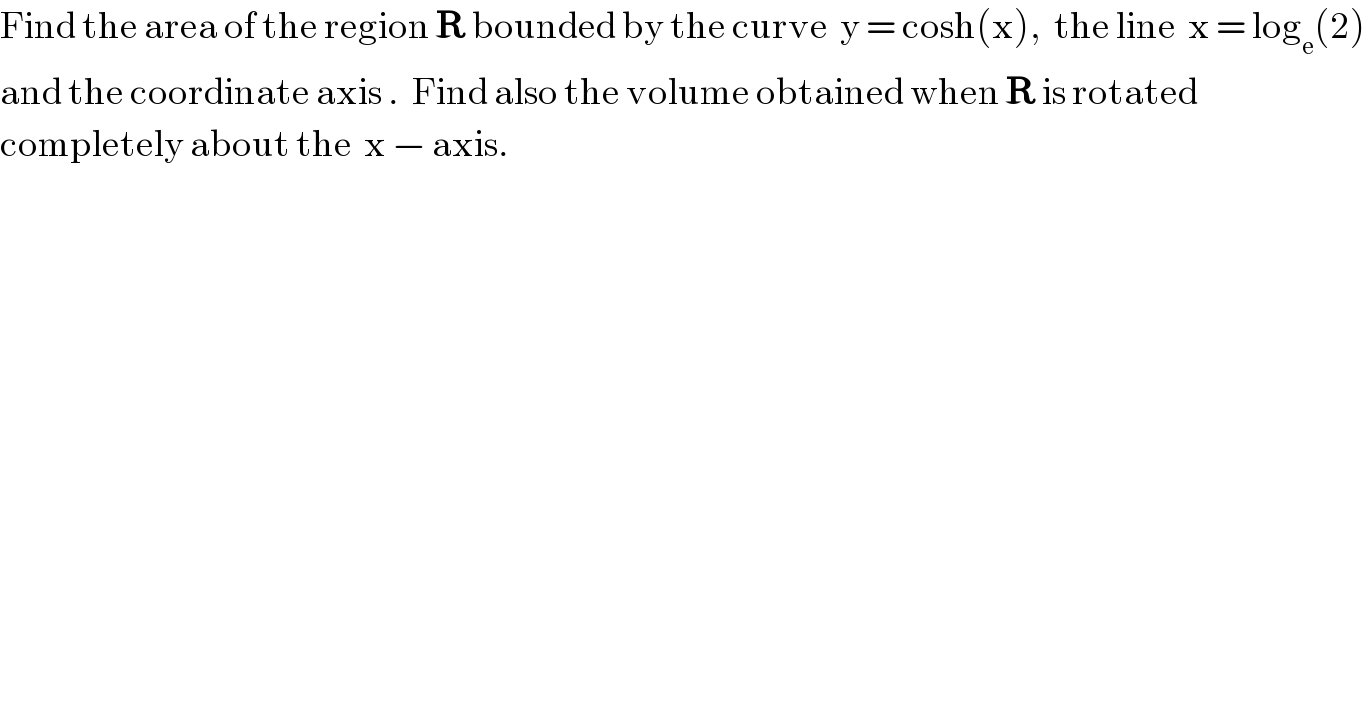
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{region}\:\boldsymbol{\mathrm{R}}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{the}\:\mathrm{curve}\:\:\mathrm{y}\:=\:\mathrm{cosh}\left(\mathrm{x}\right),\:\:\mathrm{the}\:\mathrm{line}\:\:\mathrm{x}\:=\:\mathrm{log}_{\mathrm{e}} \left(\mathrm{2}\right) \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{coordinate}\:\mathrm{axis}\:.\:\:\mathrm{Find}\:\mathrm{also}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{obtained}\:\mathrm{when}\:\boldsymbol{\mathrm{R}}\:\mathrm{is}\:\mathrm{rotated}\: \\ $$$$\mathrm{completely}\:\mathrm{about}\:\mathrm{the}\:\:\mathrm{x}\:−\:\mathrm{axis}. \\ $$
Answered by ajfour last updated on 04/Feb/18
![Area = ∫_0 ^( ln 2) (((e^x +e^(−x) )/2))dx =(1/2)(e^x −e^(−x) )∣_0 ^(ln 2) =(1/2)(2−(1/2)) =(3/4) Volume =π∫_0 ^( ln 2) (((e^x +e^(−x) )/2))^2 dx =(π/4)∫_0 ^( ln 2) (e^(2x) +e^(−2x) +2)dx =(π/4)[(e^(2x) /2)−(e^(−2x) /2)+2x]_0 ^(ln 2) =(π/8)(4−(1/4)+4ln 2) Volume = (π/(32))(15+16ln 2) .](https://www.tinkutara.com/question/Q29125.png)
$${Area}\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{ln}\:\mathrm{2}} \left(\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}\right){dx} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}} −{e}^{−{x}} \right)\mid_{\mathrm{0}} ^{\mathrm{ln}\:\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${Volume}\:=\pi\int_{\mathrm{0}} ^{\:\:\mathrm{ln}\:\mathrm{2}} \left(\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}\right)^{\mathrm{2}} {dx} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\:\mathrm{ln}\:\mathrm{2}} \left({e}^{\mathrm{2}{x}} +{e}^{−\mathrm{2}{x}} +\mathrm{2}\right){dx} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{4}}\left[\frac{{e}^{\mathrm{2}{x}} }{\mathrm{2}}−\frac{{e}^{−\mathrm{2}{x}} }{\mathrm{2}}+\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{ln}\:\mathrm{2}} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{8}}\left(\mathrm{4}−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{4ln}\:\mathrm{2}\right) \\ $$$$\:\:{Volume}\:=\:\frac{\pi}{\mathrm{32}}\left(\mathrm{15}+\mathrm{16ln}\:\mathrm{2}\right)\:. \\ $$
Commented by tawa tawa last updated on 04/Feb/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
