Menu Close

if-a-4-1-3-2-1-3-1-find-3-a-3-a-2-1-a-3-

Tinku Tara 0 Comments
Pin




Question Number 160190 by HongKing last updated on 25/Nov/21
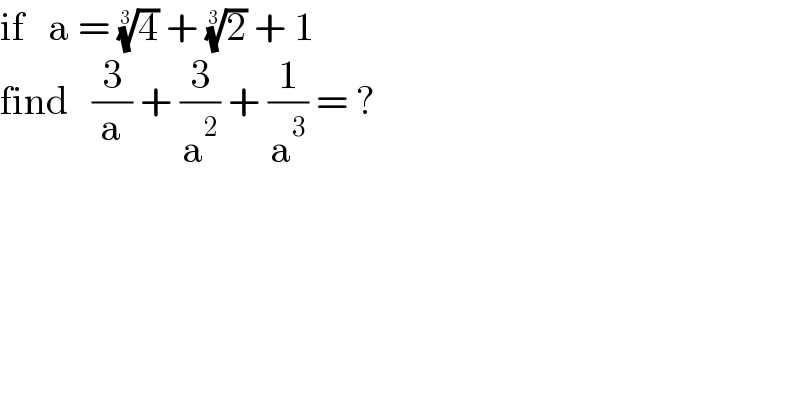
if a = (4)^(1/3) + (2)^(1/3) + 1 find (3/a) + (3/a^2 ) + (1/a^3 ) = ?
$$\mathrm{if}\:\:\:\mathrm{a}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\:\mathrm{1} \\ $$$$\mathrm{find}\:\:\:\frac{\mathrm{3}}{\mathrm{a}}\:+\:\frac{\mathrm{3}}{\mathrm{a}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\:=\:? \\ $$
Answered by amin96 last updated on 25/Nov/21
a=((((2)^(1/3) )^3 −1)/( (2)^(1/3) −1))=(1/( (2)^(1/3) −1)) (1/a)(3+(3/a)+(1/a^2 ))=((2)^(1/3) −1)(3+3(2)^(1/3) −3+((2)^(1/3) −1)^2 )= =((2)^(1/3) −1)(3(2)^(1/3) +(4)^(1/3) −2(2)^(1/3) +1)=((2)^(1/3) −1)((4)^(1/3) +(2)^(1/3) +1)= =((2)^(1/3) )^3 −1=2−1=1
$$\boldsymbol{\mathrm{a}}=\frac{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\:\:\: \\ $$$$\frac{\mathrm{1}}{{a}}\left(\mathrm{3}+\frac{\mathrm{3}}{{a}}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{3}+\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{3}+\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \right)= \\ $$$$=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}+\sqrt[{\mathrm{3}}]{\mathrm{4}}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}\right)=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}\right)= \\ $$$$=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}=\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$
Answered by mr W last updated on 25/Nov/21
a=(4)^(1/3) +(2)^(1/3) +1 a+1=(4)^(1/3) +(2)^(1/3) +2 a+1=(4)^(1/3) +(2)^(1/3) +(4)^(1/3) (2)^(1/3) a+1=((2)^(1/3) +1+(4)^(1/3) )(2)^(1/3) ((a+1)/a)=(2)^(1/3) (1+(1/a))^3 =2 1+(3/a)+(3/a^2 )+(1/a^3 )=2 ⇒(3/a)+(3/a^2 )+(1/a^3 )=1
$${a}=\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1} \\ $$$${a}+\mathrm{1}=\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{2} \\ $$$${a}+\mathrm{1}=\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$${a}+\mathrm{1}=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\right)\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\frac{{a}+\mathrm{1}}{{a}}=\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} =\mathrm{2} \\ $$$$\mathrm{1}+\frac{\mathrm{3}}{{a}}+\frac{\mathrm{3}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{3}}{{a}}+\frac{\mathrm{3}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\mathrm{1} \\ $$
Answered by 1549442205PVT last updated on 16/Dec/21
Apply a^3 −b^3 =(a−b)(a^2 +ab+b)^2 we get a = (4)^(1/3) + (2)^(1/3) + 1⇒(1/a)=(1/( (4)^(1/3) + (2)^(1/3) + 1)) =(((2)^(1/3) −1)/((^3 (√2)−1)((4)^(1/4) +^3 (√2)+1))) =(((2)^(1/3) −1)/((^3 (√2))^3 −1))=^3 (√2)−1.Hence,(1/a)+1=^3 (√2) (3/a)+(3/a^2 )+(1/a^3 )=((1/a)+1)^3 −1=(^3 (√2))^3 −1=1
$${Apply}\:{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}\right)^{\mathrm{2}} {we}\:{get} \\ $$$$\mathrm{a}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\:\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{a}}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\:\mathrm{1}} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{4}}+^{\mathrm{3}} \sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}}=^{\mathrm{3}} \sqrt{\mathrm{2}}−\mathrm{1}.{Hence},\frac{\mathrm{1}}{{a}}+\mathrm{1}=^{\mathrm{3}} \sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{{a}}+\frac{\mathrm{3}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\left(\frac{\mathrm{1}}{{a}}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}=\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}=\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *