Question Number 94811 by Abdulrahman last updated on 21/May/20
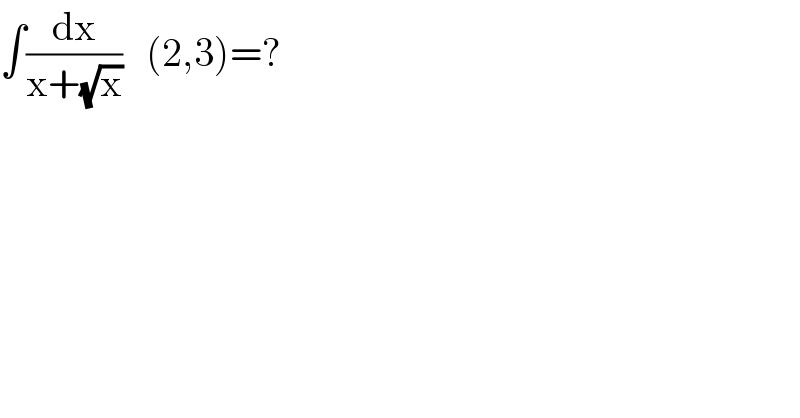
$$\int\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}}}\:\:\:\left(\mathrm{2},\mathrm{3}\right)=? \\ $$
Answered by ElOuafi last updated on 21/May/20
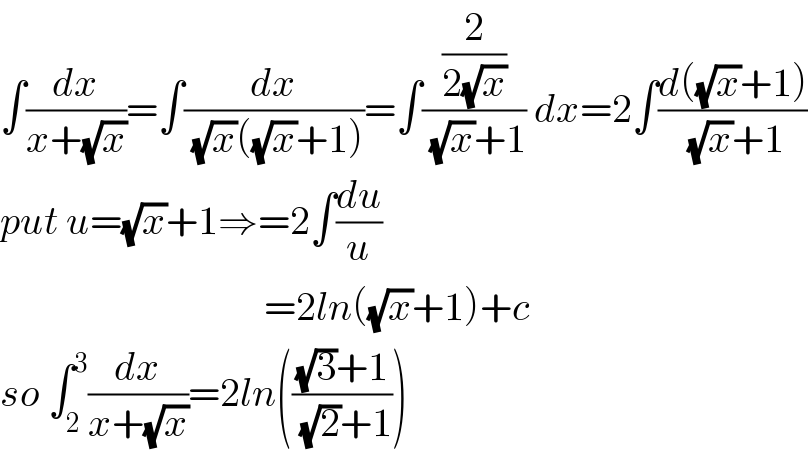
$$\int\frac{{dx}}{{x}+\sqrt{{x}}}=\int\frac{{dx}}{\:\sqrt{{x}}\left(\sqrt{{x}}+\mathrm{1}\right)}=\int\frac{\frac{\mathrm{2}}{\mathrm{2}\sqrt{{x}}}}{\:\sqrt{{x}}+\mathrm{1}}\:{dx}=\mathrm{2}\int\frac{{d}\left(\sqrt{{x}}+\mathrm{1}\right)}{\:\sqrt{{x}}+\mathrm{1}} \\ $$$${put}\:{u}=\sqrt{{x}}+\mathrm{1}\Rightarrow=\mathrm{2}\int\frac{{du}}{{u}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{ln}\left(\sqrt{{x}}+\mathrm{1}\right)+{c} \\ $$$${so}\:\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{dx}}{{x}+\sqrt{{x}}}=\mathrm{2}{ln}\left(\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right) \\ $$
Commented by Abdulrahman last updated on 21/May/20

$$\mathrm{thanks}\:\mathrm{alot} \\ $$
Answered by i jagooll last updated on 21/May/20
![let (√(x ))=t ⇒x=t^2 ; dx = 2t dt ∫ ((2t dt)/(t^2 +t)) = ∫ ((2 dt)/(t+1)) = 2 ln ∣t+1∣ = 2[ ln ∣1+(√x) ∣ ]_2 ^3 = 2 {ln (1+(√3))−ln(1+(√2)) } = 2 ln (((1+(√3))/(1+(√2))))](https://www.tinkutara.com/question/Q94821.png)
$$\mathrm{let}\:\sqrt{\mathrm{x}\:}=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\mathrm{2}} \:;\:\mathrm{dx}\:=\:\mathrm{2t}\:\mathrm{dt}\: \\ $$$$\int\:\:\frac{\mathrm{2t}\:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}}\:=\:\int\:\frac{\mathrm{2}\:\mathrm{dt}}{\mathrm{t}+\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{ln}\:\mid\mathrm{t}+\mathrm{1}\mid \\ $$$$=\:\mathrm{2}\left[\:\:\mathrm{ln}\:\mid\mathrm{1}+\sqrt{\mathrm{x}}\:\mid\:\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\:\mathrm{2}\:\left\{\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\right\}\: \\ $$$$=\:\mathrm{2}\:\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)\: \\ $$
Commented by Abdulrahman last updated on 21/May/20

$$\mathrm{thanks}\:\mathrm{alot} \\ $$
Answered by mathmax by abdo last updated on 21/May/20
![I =∫_2 ^3 (dx/(x+(√x))) we do the changement (√x)=t ⇒ I =∫_(√2) ^(√3) ((2tdt)/(t^2 +t)) =2 ∫_(√2) ^(√3) (dt/(t+1)) =2[ln(t+1)]_(√2) ^(√3) =2(ln(1+(√3))−ln(1+(√2)))](https://www.tinkutara.com/question/Q94898.png)
$$\mathrm{I}\:=\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}}\:=\mathrm{2}\:\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{1}}\:=\mathrm{2}\left[\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)\right]_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} \:=\mathrm{2}\left(\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right) \\ $$
