Question Number 160451 by Ar Brandon last updated on 29/Nov/21

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{system}\:\mathrm{below}: \\ $$$$\begin{cases}{{y}_{\mathrm{1}} '=\mathrm{2}{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +{y}_{\mathrm{3}} }\\{{y}_{\mathrm{2}} '=−\mathrm{2}{y}_{\mathrm{1}} −{y}_{\mathrm{3}} }\\{{y}_{\mathrm{3}} '=\mathrm{2}{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +\mathrm{2}{y}_{\mathrm{3}} }\end{cases} \\ $$
Answered by mr W last updated on 30/Nov/21
![GENERAL METHOD determinant (((2−λ),1,1),((−2),(−λ),(−1)),(2,1,(2−λ)))=0 (2−λ)(λ^2 −2λ+1)=0 ⇒λ_1 =2, λ_2 =λ_3 =1 V_1 = [(1),((−2)),(2) ] V_2 = [(0),(1),((−1)) ] V_3 = [(0),((−1)),(1) ] ⇒ [(y_1 ),(y_2 ),(y_3 ) ]=C_1 e^(2x) [(1),((−2)),(2) ]+C_2 e^x [(0),(1),((−1)) ]+C_3 e^x [(0),((−1)),(1) ] or y_1 =C_1 e^(2x) y_2 =−2C_1 e^(2x) +C_2 e^x y_3 =−y_2](https://www.tinkutara.com/question/Q160474.png)
$${GENERAL}\:{METHOD} \\ $$$$ \\ $$$$\begin{vmatrix}{\mathrm{2}−\lambda}&{\mathrm{1}}&{\mathrm{1}}\\{−\mathrm{2}}&{−\lambda}&{−\mathrm{1}}\\{\mathrm{2}}&{\mathrm{1}}&{\mathrm{2}−\lambda}\end{vmatrix}=\mathrm{0} \\ $$$$\left(\mathrm{2}−\lambda\right)\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda_{\mathrm{1}} =\mathrm{2},\:\lambda_{\mathrm{2}} =\lambda_{\mathrm{3}} =\mathrm{1} \\ $$$${V}_{\mathrm{1}} =\begin{bmatrix}{\mathrm{1}}\\{−\mathrm{2}}\\{\mathrm{2}}\end{bmatrix} \\ $$$${V}_{\mathrm{2}} =\begin{bmatrix}{\mathrm{0}}\\{\mathrm{1}}\\{−\mathrm{1}}\end{bmatrix} \\ $$$${V}_{\mathrm{3}} =\begin{bmatrix}{\mathrm{0}}\\{−\mathrm{1}}\\{\mathrm{1}}\end{bmatrix} \\ $$$$\Rightarrow\begin{bmatrix}{{y}_{\mathrm{1}} }\\{{y}_{\mathrm{2}} }\\{{y}_{\mathrm{3}} }\end{bmatrix}={C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} \begin{bmatrix}{\mathrm{1}}\\{−\mathrm{2}}\\{\mathrm{2}}\end{bmatrix}+{C}_{\mathrm{2}} {e}^{{x}} \begin{bmatrix}{\mathrm{0}}\\{\mathrm{1}}\\{−\mathrm{1}}\end{bmatrix}+{C}_{\mathrm{3}} {e}^{{x}} \begin{bmatrix}{\mathrm{0}}\\{−\mathrm{1}}\\{\mathrm{1}}\end{bmatrix} \\ $$$${or} \\ $$$${y}_{\mathrm{1}} ={C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} \\ $$$${y}_{\mathrm{2}} =−\mathrm{2}{C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{C}_{\mathrm{2}} {e}^{{x}} \\ $$$${y}_{\mathrm{3}} =−{y}_{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 30/Nov/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by mr W last updated on 30/Nov/21

$${i}\:{need}\:{to}\:{check}\:{the}\:{working},\:{maybe} \\ $$$${there}\:{is}\:{a}\:{mistake}\:{inside}. \\ $$
Answered by mr W last updated on 30/Nov/21
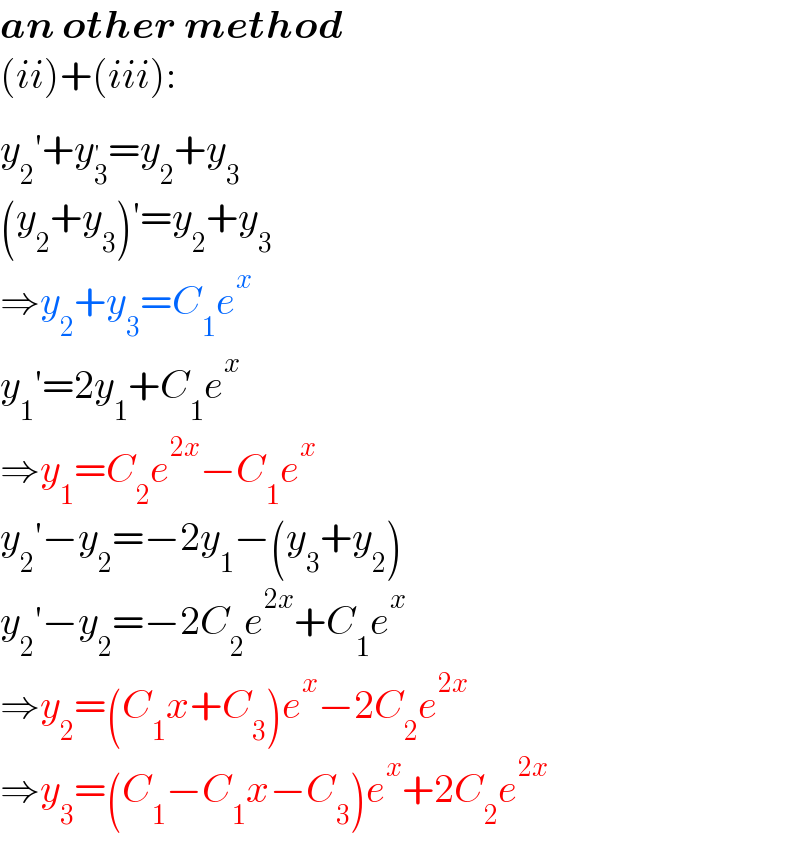
$$\boldsymbol{{an}}\:\boldsymbol{{other}}\:\boldsymbol{{method}} \\ $$$$\left({ii}\right)+\left({iii}\right): \\ $$$${y}_{\mathrm{2}} '+{y}_{\mathrm{3}} ^{'} ={y}_{\mathrm{2}} +{y}_{\mathrm{3}} \\ $$$$\left({y}_{\mathrm{2}} +{y}_{\mathrm{3}} \right)'={y}_{\mathrm{2}} +{y}_{\mathrm{3}} \\ $$$$\Rightarrow{y}_{\mathrm{2}} +{y}_{\mathrm{3}} ={C}_{\mathrm{1}} {e}^{{x}} \\ $$$${y}_{\mathrm{1}} '=\mathrm{2}{y}_{\mathrm{1}} +{C}_{\mathrm{1}} {e}^{{x}} \\ $$$$\Rightarrow{y}_{\mathrm{1}} ={C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} −{C}_{\mathrm{1}} {e}^{{x}} \\ $$$${y}_{\mathrm{2}} '−{y}_{\mathrm{2}} =−\mathrm{2}{y}_{\mathrm{1}} −\left({y}_{\mathrm{3}} +{y}_{\mathrm{2}} \right) \\ $$$${y}_{\mathrm{2}} '−{y}_{\mathrm{2}} =−\mathrm{2}{C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} +{C}_{\mathrm{1}} {e}^{{x}} \\ $$$$\Rightarrow{y}_{\mathrm{2}} =\left({C}_{\mathrm{1}} {x}+{C}_{\mathrm{3}} \right){e}^{{x}} −\mathrm{2}{C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} \\ $$$$\Rightarrow{y}_{\mathrm{3}} =\left({C}_{\mathrm{1}} −{C}_{\mathrm{1}} {x}−{C}_{\mathrm{3}} \right){e}^{{x}} +\mathrm{2}{C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} \\ $$
