Question Number 29384 by NECx last updated on 08/Feb/18
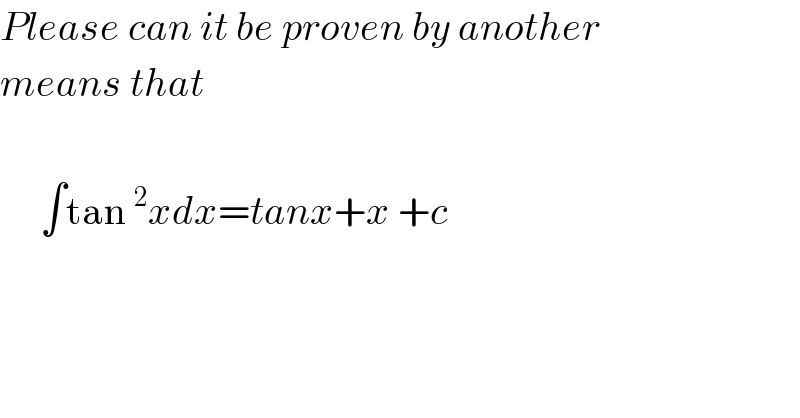
$${Please}\:{can}\:{it}\:{be}\:{proven}\:{by}\:{another} \\ $$$${means}\:{that}\: \\ $$$$ \\ $$$$\:\:\:\:\:\int\mathrm{tan}\:^{\mathrm{2}} {xdx}={tanx}+{x}\:+{c} \\ $$
Commented by abdo imad last updated on 08/Feb/18
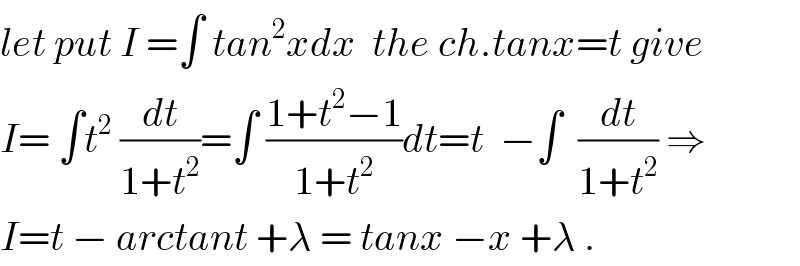
$${let}\:{put}\:{I}\:=\int\:{tan}^{\mathrm{2}} {xdx}\:\:{the}\:{ch}.{tanx}={t}\:{give} \\ $$$${I}=\:\int{t}^{\mathrm{2}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\int\:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={t}\:\:−\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}={t}\:−\:{arctant}\:+\lambda\:=\:{tanx}\:−{x}\:+\lambda\:. \\ $$
Commented by abdo imad last updated on 08/Feb/18
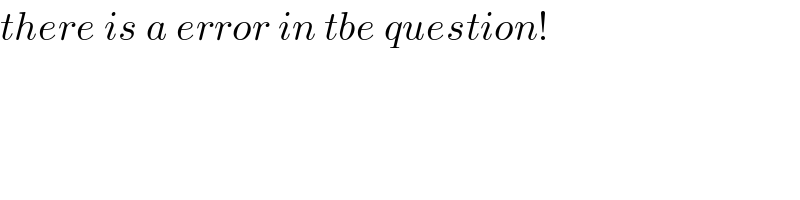
$${there}\:{is}\:{a}\:{error}\:{in}\:{tbe}\:{question}! \\ $$
Commented by NECx last updated on 08/Feb/18

$${wow}….\:{Thanks} \\ $$
