Question Number 160457 by HongKing last updated on 29/Nov/21

$$\mathrm{Simplfy}: \\ $$$$\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\::\:\left(\mathrm{1}\:+\:\left(\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}\boldsymbol{\alpha}}\right)^{\mathrm{2}} \right) \\ $$
Answered by MJS_new last updated on 29/Nov/21
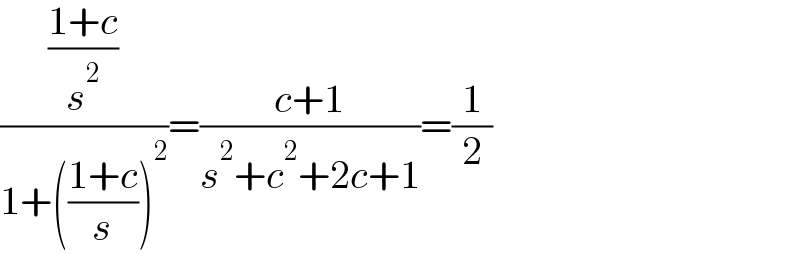
$$\frac{\frac{\mathrm{1}+{c}}{{s}^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{1}+{c}}{{s}}\right)^{\mathrm{2}} }=\frac{{c}+\mathrm{1}}{{s}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{c}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 30/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Nov/21
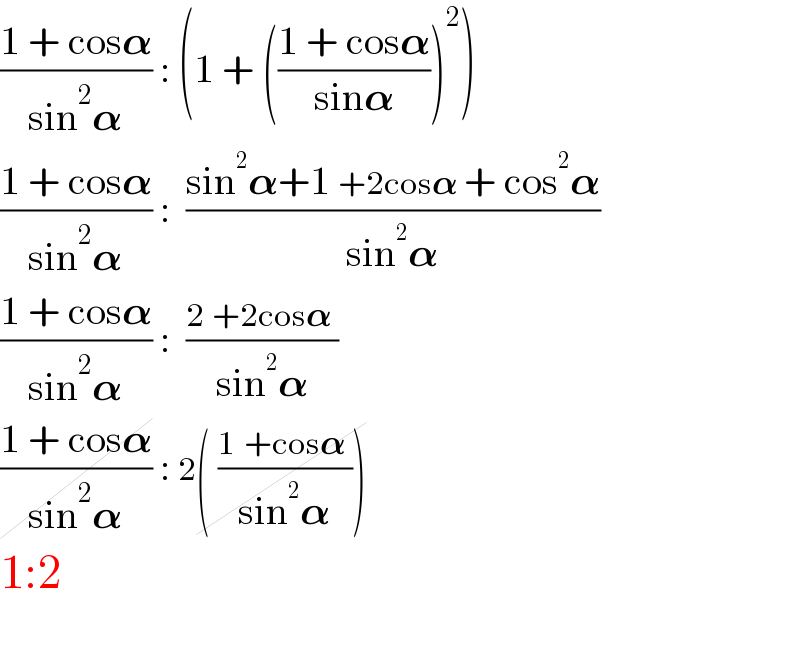
$$\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\::\:\left(\mathrm{1}\:+\:\left(\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}\boldsymbol{\alpha}}\right)^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\::\:\:\frac{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}+\mathrm{1}\:+\mathrm{2cos}\boldsymbol{\alpha}\:+\:\mathrm{cos}^{\mathrm{2}} \boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}} \\ $$$$\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\::\:\:\frac{\mathrm{2}\:+\mathrm{2cos}\boldsymbol{\alpha}\:}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}} \\ $$$$\cancel{\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}}\::\:\mathrm{2}\cancel{\left(\:\frac{\mathrm{1}\:+\mathrm{cos}\boldsymbol{\alpha}\:}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\right)} \\ $$$$\mathrm{1}:\mathrm{2} \\ $$$$ \\ $$
Commented by HongKing last updated on 30/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
