Question Number 133782 by bramlexs22 last updated on 24/Feb/21
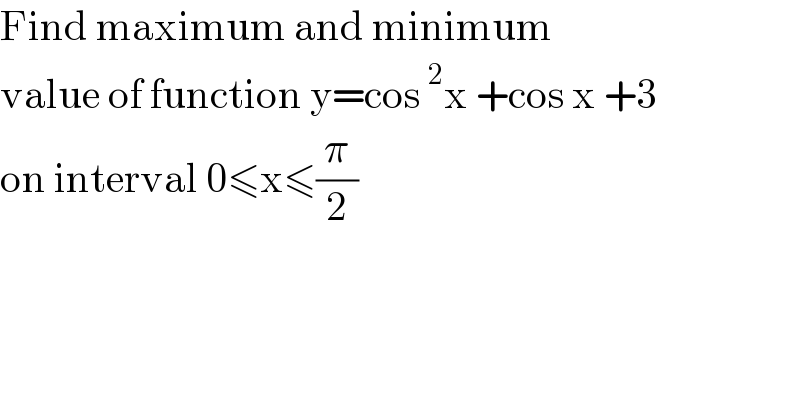
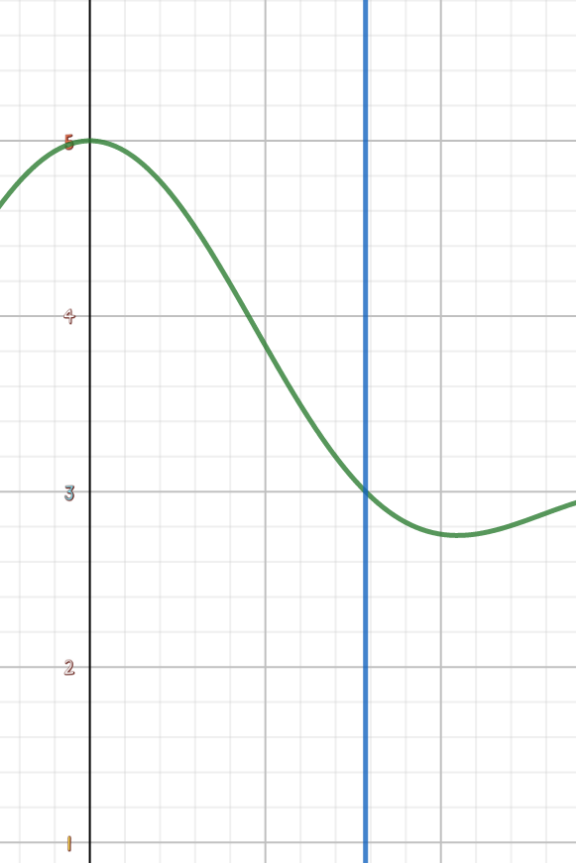
$$\mathrm{Find}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum}\: \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{function}\:\mathrm{y}=\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:+\mathrm{cos}\:\mathrm{x}\:+\mathrm{3}\: \\ $$$$\mathrm{on}\:\mathrm{interval}\:\mathrm{0}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 24/Feb/21
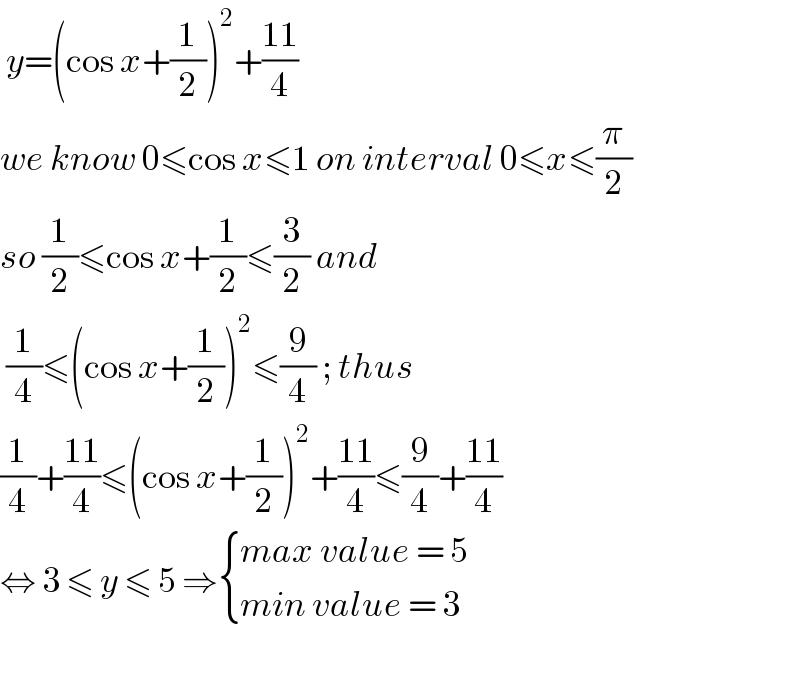
$$\:{y}=\left(\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}} \\ $$$${we}\:{know}\:\mathrm{0}\leqslant\mathrm{cos}\:{x}\leqslant\mathrm{1}\:{on}\:{interval}\:\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$${so}\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{3}}{\mathrm{2}}\:{and}\: \\ $$$$\:\frac{\mathrm{1}}{\mathrm{4}}\leqslant\left(\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \leqslant\frac{\mathrm{9}}{\mathrm{4}}\:;\:{thus}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{11}}{\mathrm{4}}\leqslant\left(\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}\leqslant\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\Leftrightarrow\:\mathrm{3}\:\leqslant\:{y}\:\leqslant\:\mathrm{5}\:\Rightarrow\begin{cases}{{max}\:{value}\:=\:\mathrm{5}}\\{{min}\:{value}\:=\:\mathrm{3}}\end{cases} \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 24/Feb/21