Question Number 68244 by mathmax by abdo last updated on 07/Sep/19
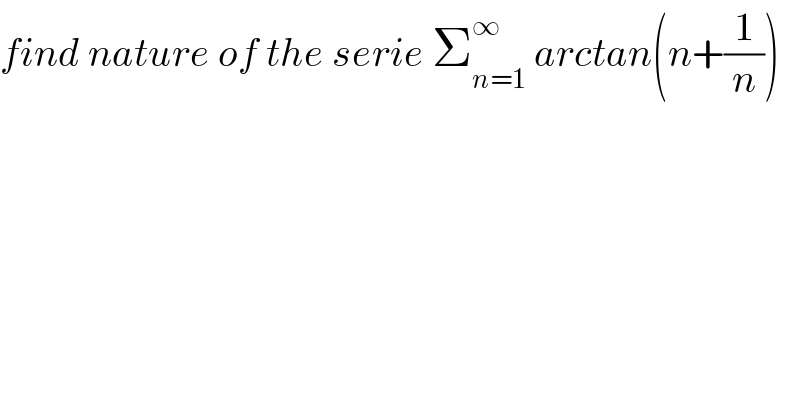
$${find}\:{nature}\:{of}\:{the}\:{serie}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{arctan}\left({n}+\frac{\mathrm{1}}{{n}}\right) \\ $$
Commented by mathmax by abdo last updated on 23/Sep/19

$${let}\:{u}_{{n}} ={arctan}\left({n}+\frac{\mathrm{1}}{{n}}\right)\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} =\frac{\pi}{\mathrm{2}}\:\neq\mathrm{0}\:\Rightarrow\Sigma\:{u}_{{n}} {diverges} \\ $$
