Menu Close

solve-0-tan-1-x-1-x-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 160547 by mnjuly1970 last updated on 01/Dec/21
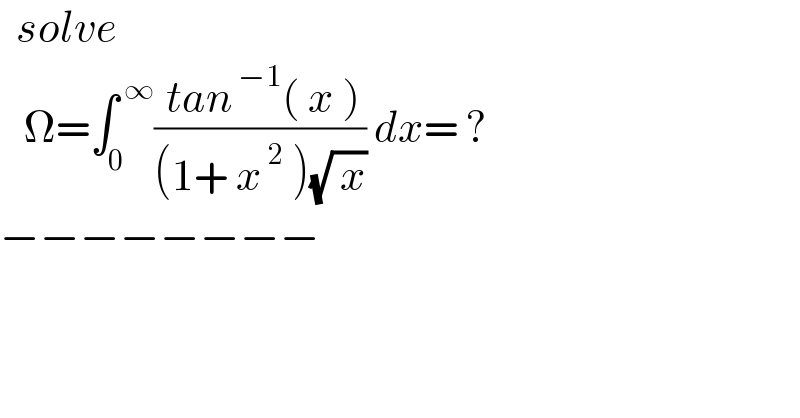
solve Ω=∫_0 ^( ∞) (( tan^( −1) ( x ))/((1+ x^( 2) )(√( x)))) dx= ? −−−−−−−−
$$\:\:{solve} \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{\:{tan}^{\:−\mathrm{1}} \left(\:{x}\:\right)}{\left(\mathrm{1}+\:{x}^{\:\mathrm{2}} \:\right)\sqrt{\:{x}}}\:{dx}=\:? \\ $$$$−−−−−−−− \\ $$
Answered by Kamel last updated on 01/Dec/21
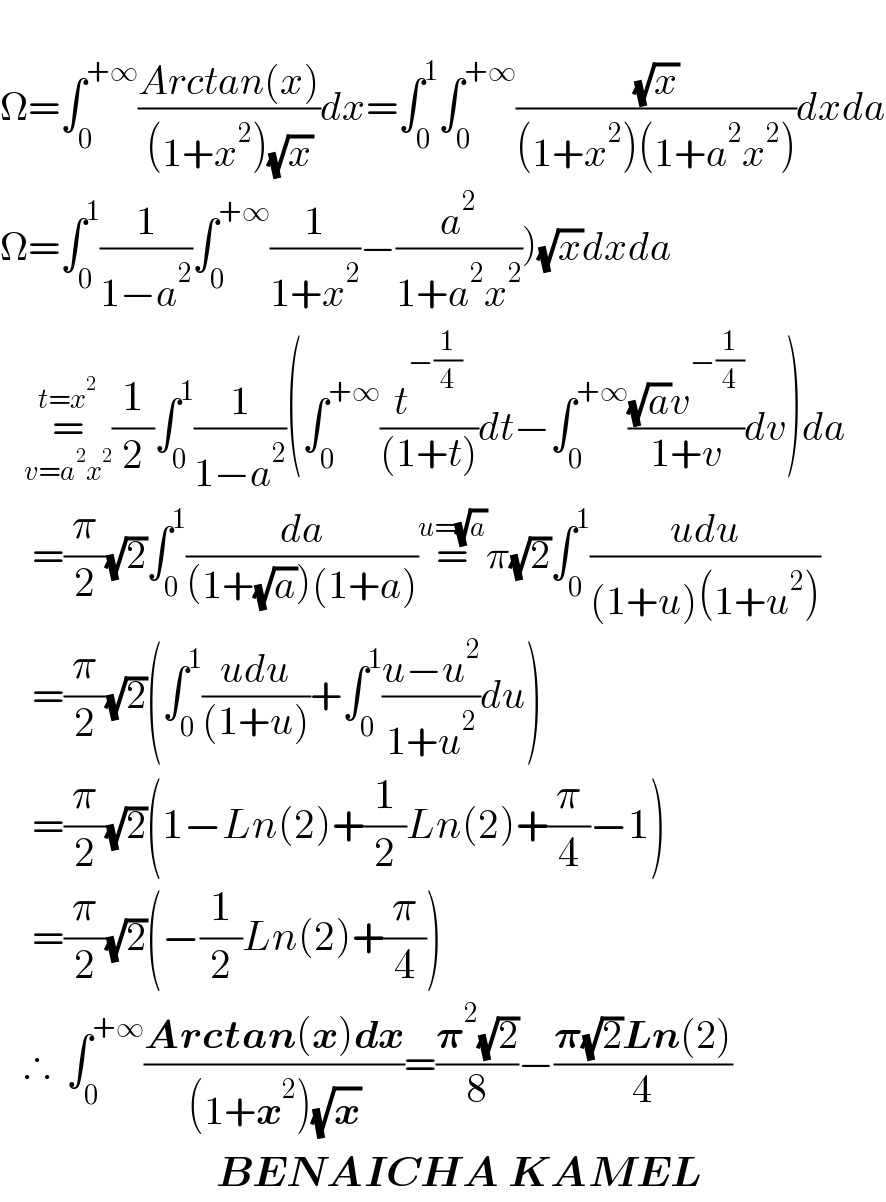
Ω=∫_0 ^(+∞) ((Arctan(x))/((1+x^2 )(√x)))dx=∫_0 ^1 ∫_0 ^(+∞) ((√x)/((1+x^2 )(1+a^2 x^2 )))dxda Ω=∫_0 ^1 (1/(1−a^2 ))∫_0 ^(+∞) (1/(1+x^2 ))−(a^2 /(1+a^2 x^2 )))(√x)dxda =_(v=a^2 x^2 ) ^(t=x^2 ) (1/2)∫_0 ^1 (1/(1−a^2 ))(∫_0 ^(+∞) (t^(−(1/4)) /((1+t)))dt−∫_0 ^(+∞) (((√a)v^(−(1/4)) )/(1+v))dv)da =(π/2)(√2)∫_0 ^1 (da/((1+(√a))(1+a)))=^(u=(√a)) π(√2)∫_0 ^1 ((udu)/((1+u)(1+u^2 ))) =(π/2)(√2)(∫_0 ^1 ((udu)/((1+u)))+∫_0 ^1 ((u−u^2 )/(1+u^2 ))du) =(π/2)(√2)(1−Ln(2)+(1/2)Ln(2)+(π/4)−1) =(π/2)(√2)(−(1/2)Ln(2)+(π/4)) ∴ ∫_0 ^(+∞) ((Arctan(x)dx)/((1+x^2 )(√x)))=((𝛑^2 (√2))/8)−((𝛑(√2)Ln(2))/4) BENAICHA KAMEL
$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{{Arctan}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{+\infty} \frac{\sqrt{{x}}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{dxda} \\ $$$$\left.\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }\right)\sqrt{{x}}{dxda} \\ $$$$\:\:\:\underset{{v}={a}^{\mathrm{2}} {x}^{\mathrm{2}} } {\overset{{t}={x}^{\mathrm{2}} } {=}}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\left(\int_{\mathrm{0}} ^{+\infty} \frac{{t}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{1}+{t}\right)}{dt}−\int_{\mathrm{0}} ^{+\infty} \frac{\sqrt{{a}}{v}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}+{v}}{dv}\right){da} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{da}}{\left(\mathrm{1}+\sqrt{{a}}\right)\left(\mathrm{1}+{a}\right)}\overset{{u}=\sqrt{{a}}} {=}\pi\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{udu}}{\left(\mathrm{1}+{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}}\sqrt{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{udu}}{\left(\mathrm{1}+{u}\right)}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du}\right) \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}}\sqrt{\mathrm{2}}\left(\mathrm{1}−{Ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}{Ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}−\mathrm{1}\right) \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}}\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}{Ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\:\:\:\therefore\:\:\int_{\mathrm{0}} ^{+\infty} \frac{\boldsymbol{{Arctan}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)\sqrt{\boldsymbol{{x}}}}=\frac{\boldsymbol{\pi}^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\boldsymbol{\pi}\sqrt{\mathrm{2}}\boldsymbol{{Ln}}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{BENAICHA}}\:\boldsymbol{{KAMEL}} \\ $$
Commented by mnjuly1970 last updated on 01/Dec/21
tashakor ..sir kamel
$$\:\:\:\:\:\:{tashakor}\:..{sir}\:{kamel} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *