Question Number 133786 by bobhans last updated on 24/Feb/21
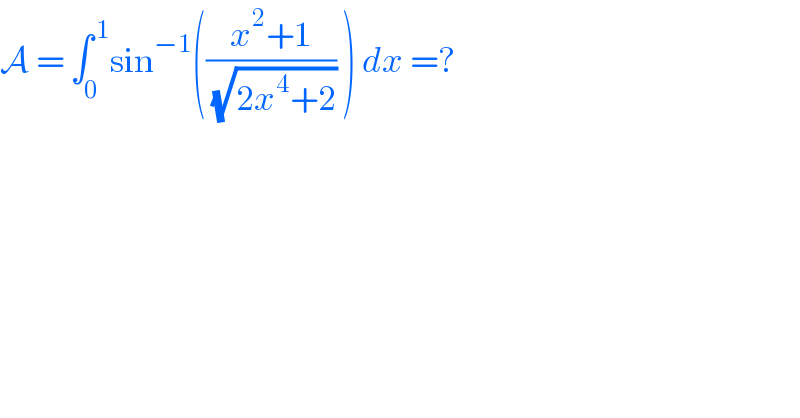
$$\mathcal{A}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}}}\:\right)\:{dx}\:=? \\ $$
Answered by john_santu last updated on 24/Feb/21
![Using the Pythagorean theorem arcsin (((x^2 +1)/( (√(2x^4 +2)))) )=arctan (((1+x^2 )/(1−x^2 )) ) A=∫_0 ^( 1) arctan (((1+x^2 )/(1−x^2 )) )dx Use by integration by parts A= x arctan (((1+x^2 )/(1−x^2 ))) ∣_0 ^1 −2∫_0 ^( 1) (x^2 /(x^4 +1)) dx A= (π/2)−[∫_0 ^( 1) ((1+(1/x^2 ))/(x^2 +(1/x^2 ))) dx +∫_0 ^( 1) ((1−(1/x^2 ))/(x^2 +(1/x^2 ))) dx ] A=(π/2)−(1/(2(√2))) (π+ln (3)−2(√2) ) A ≈ 1.0833](https://www.tinkutara.com/question/Q133790.png)
$${Using}\:{the}\:{Pythagorean}\:{theorem}\: \\ $$$$\mathrm{arcsin}\:\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}}}\:\right)=\mathrm{arctan}\:\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:\right) \\ $$$$\mathcal{A}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{arctan}\:\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:\right){dx}\: \\ $$$${Use}\:{by}\:\:{integration}\:{by}\:{parts} \\ $$$$\mathcal{A}=\:{x}\:\mathrm{arctan}\:\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx} \\ $$$$\mathcal{A}=\:\frac{\pi}{\mathrm{2}}−\left[\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx}\:+\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx}\:\right] \\ $$$$\mathcal{A}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\left(\pi+\mathrm{ln}\:\left(\mathrm{3}\right)−\mathrm{2}\sqrt{\mathrm{2}}\:\right) \\ $$$$\mathcal{A}\:\approx\:\mathrm{1}.\mathrm{0833}\: \\ $$
