Find-1-ln-x-x-4-x-2-1-dx-

Question Number 160560 by HongKing last updated on 01/Dec/21

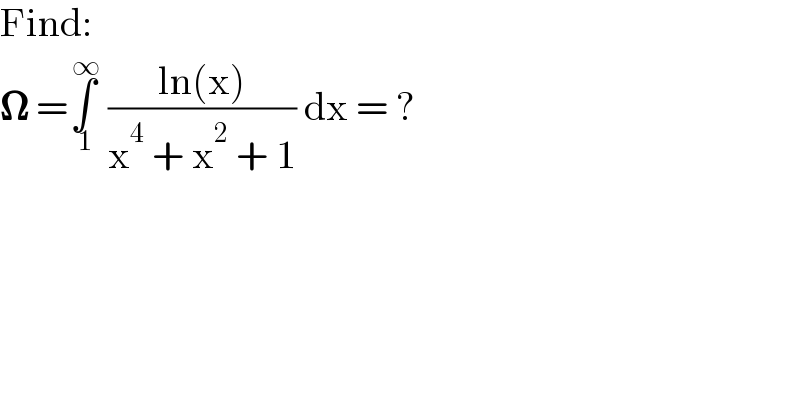
Find: 𝛀 =∫_( 1) ^( ∞) ((ln(x))/(x^4 + x^2 + 1)) dx = ?

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{1}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:\mathrm{dx}\:=\:? \\ $$

Answered by Ar Brandon last updated on 02/Dec/21

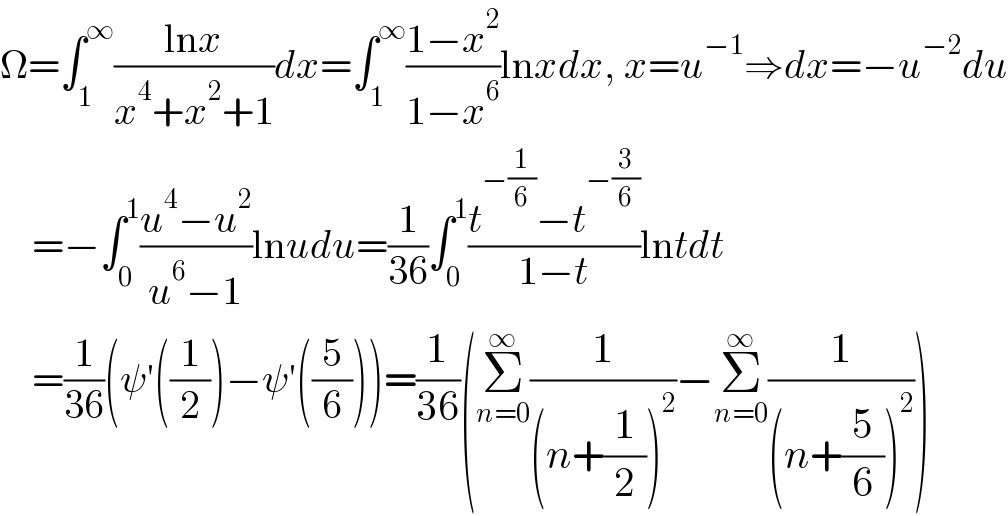
Ω=∫_1 ^∞ ((lnx)/(x^4 +x^2 +1))dx=∫_1 ^∞ ((1−x^2 )/(1−x^6 ))lnxdx, x=u^(−1) ⇒dx=−u^(−2) du =−∫_0 ^1 ((u^4 −u^2 )/(u^6 −1))lnudu=(1/(36))∫_0 ^1 ((t^(−(1/6)) −t^(−(3/6)) )/(1−t))lntdt =(1/(36))(ψ′((1/2))−ψ′((5/6)))=(1/(36))(Σ_(n=0) ^∞ (1/((n+(1/2))^2 ))−Σ_(n=0) ^∞ (1/((n+(5/6))^2 )))

$$\Omega=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{6}} }\mathrm{ln}{xdx},\:{x}={u}^{−\mathrm{1}} \Rightarrow{dx}=−{u}^{−\mathrm{2}} {du} \\ $$$$\:\:\:\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{4}} −{u}^{\mathrm{2}} }{{u}^{\mathrm{6}} −\mathrm{1}}\mathrm{ln}{udu}=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{−\frac{\mathrm{1}}{\mathrm{6}}} −{t}^{−\frac{\mathrm{3}}{\mathrm{6}}} }{\mathrm{1}−{t}}\mathrm{ln}{tdt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{36}}\left(\psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi'\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\right)=\frac{\mathrm{1}}{\mathrm{36}}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{2}} }\right) \\ $$

Commented by HongKing last updated on 02/Dec/21

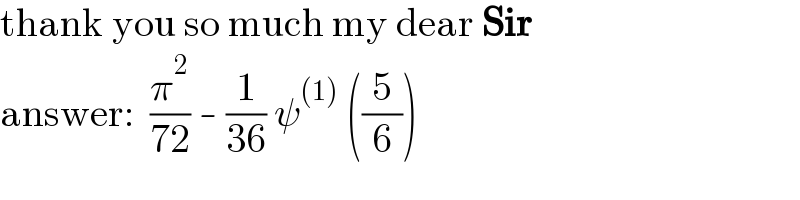
thank you so much my dear Sir answer: (π^2 /(72)) - (1/(36)) ψ^((1)) ((5/6))

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Sir}} \\ $$$$\mathrm{answer}:\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{72}}\:-\:\frac{\mathrm{1}}{\mathrm{36}}\:\psi^{\left(\mathrm{1}\right)} \:\left(\frac{\mathrm{5}}{\mathrm{6}}\right) \\ $$

Commented by Ar Brandon last updated on 02/Dec/21

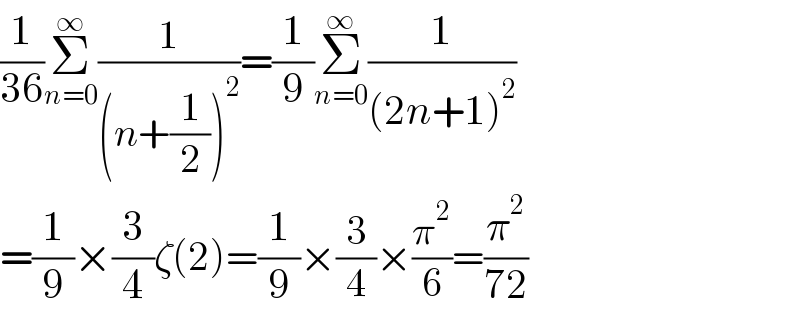
(1/(36))Σ_(n=0) ^∞ (1/((n+(1/2))^2 ))=(1/9)Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(1/9)×(3/4)ζ(2)=(1/9)×(3/4)×(π^2 /6)=(π^2 /(72))

$$\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}×\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{9}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{72}} \\ $$

Commented by HongKing last updated on 02/Dec/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Sir}} \\ $$

Facebook Tweet Pin

Find-1-ln-x-x-4-x-2-1-dx-

Leave a Reply Cancel reply