Question Number 2720 by prakash jain last updated on 25/Nov/15

$$\mathrm{Analytical}\:\mathrm{Continuation} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{below}\:\mathrm{divergent}\:\mathrm{series}\:\mathrm{was} \\ $$$$\mathrm{shown}\:\mathrm{to}\:\mathrm{be}\:\mathrm{using}\:\mathrm{analytical}\:\mathrm{continuation}. \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{i}−\mathrm{1}} =−\mathrm{1}\:\:\:\:\:\:…\left(\mathrm{A}\right) \\ $$$$\zeta\left(−\mathrm{1}\right)=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}{i}=−\frac{\mathrm{1}}{\mathrm{12}}\:\:\:\:\:\:…\left(\mathrm{B}\right) \\ $$$$\mathrm{While}\:\mathrm{reading}\:\mathrm{about}\:\mathrm{analytical}\:\mathrm{continuation}, \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{the}\:\mathrm{found}\:\mathrm{the}\:\mathrm{following}: \\ $$$$\mathrm{If}\:{f}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{function}\:\mathrm{over}\:\mathrm{domain}\:\mathrm{D}_{\mathrm{1}} \:\mathrm{and} \\ $$$$\mathrm{If}\:{f}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{function}\:\mathrm{over}\:\mathrm{domain}\:\mathrm{D}_{\mathrm{2}} \:\mathrm{and} \\ $$$${f}_{\mathrm{1}} ={f}_{\mathrm{2}} \:\mathrm{on}\:\mathrm{D}_{\mathrm{1}} \cap\mathrm{D}_{\mathrm{2}} ,\:{f}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{called}\:\mathrm{analytical}\: \\ $$$$\mathrm{continuation}\:\mathrm{of}\:{f}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{vice}\:\mathrm{versa}. \\ $$$$\boldsymbol{\mathrm{Question}}: \\ $$$$\mathrm{In}\:\mathrm{case}\:\mathrm{of}\:\mathrm{series}\:\left(\mathrm{A}\right)\:\mathrm{and}\:\left(\mathrm{B}\right)\:\mathrm{above}\:\mathrm{what}\:\mathrm{function} \\ $$$$\mathrm{is}\:\mathrm{used}\:\mathrm{as}\:{f}_{\mathrm{2}} \:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{also}\:\mathrm{what}\:\mathrm{is}\:\mathrm{used}\:\mathrm{as}\:{f}_{\mathrm{1}} ? \\ $$
Commented by prakash jain last updated on 25/Nov/15

$$\mathrm{There}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{question}\:\mathrm{below}\:\mathrm{by}\:\mathrm{Filup}\:\mathrm{about} \\ $$$$\mathrm{definition}\:\mathrm{of}\:\zeta\left({s}\right)\:\mathrm{for}\:{s}<\mathrm{1}\:\mathrm{using}\:\mathrm{analytical} \\ $$$$\mathrm{continuity}. \\ $$
Answered by 123456 last updated on 26/Nov/15

$$\mathrm{for}\:\mathrm{A} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{+\infty} {\sum}}{x}^{{i}} \\ $$$${f}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} =\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\mid{x}\mid<\mathrm{1}\Rightarrow{x}^{{n}+\mathrm{1}} \rightarrow\mathrm{0}\Rightarrow{f}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{0}−\mathrm{1}}{{x}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${f}_{\mathrm{1}} \left({x}\right)={f}_{\mathrm{2}} \left({x}\right)\:\mid{x}\mid<\mathrm{1},\:\mathrm{so}\:{f}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{continuation} \\ $$
Commented by 123456 last updated on 26/Nov/15
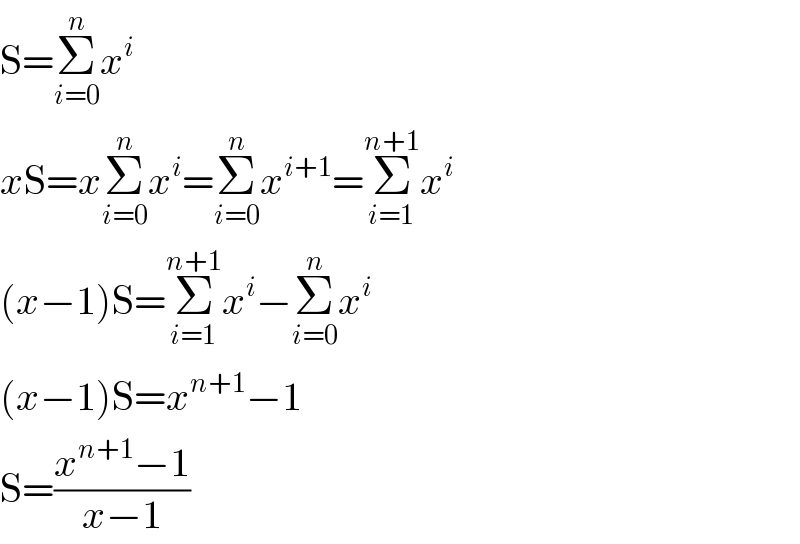
$$\mathrm{S}=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} \\ $$$${x}\mathrm{S}={x}\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}+\mathrm{1}} =\underset{{i}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{x}^{{i}} \\ $$$$\left({x}−\mathrm{1}\right)\mathrm{S}=\underset{{i}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{x}^{{i}} −\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} \\ $$$$\left({x}−\mathrm{1}\right)\mathrm{S}={x}^{{n}+\mathrm{1}} −\mathrm{1} \\ $$$$\mathrm{S}=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$
Commented by prakash jain last updated on 26/Nov/15

$$\mathrm{Thank}\:\mathrm{You}. \\ $$
