Menu Close

y-x-2-y-2-x-x-2-y-2-dx-y-x-2-y-2-x-x-2-y-2-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 95098 by i jagooll last updated on 23/May/20
[ (y/(x^2 +y^2 )) + (x/(x^2 +y^2 )) ] dx + [(y/(x^2 +y^2 ))−(x/(x^2 +y^2 )) ]dy=0
$$\left[\:\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:+\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\:\mathrm{dx}\:+\:\left[\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\mathrm{dy}=\mathrm{0} \\ $$
Answered by bobhans last updated on 23/May/20
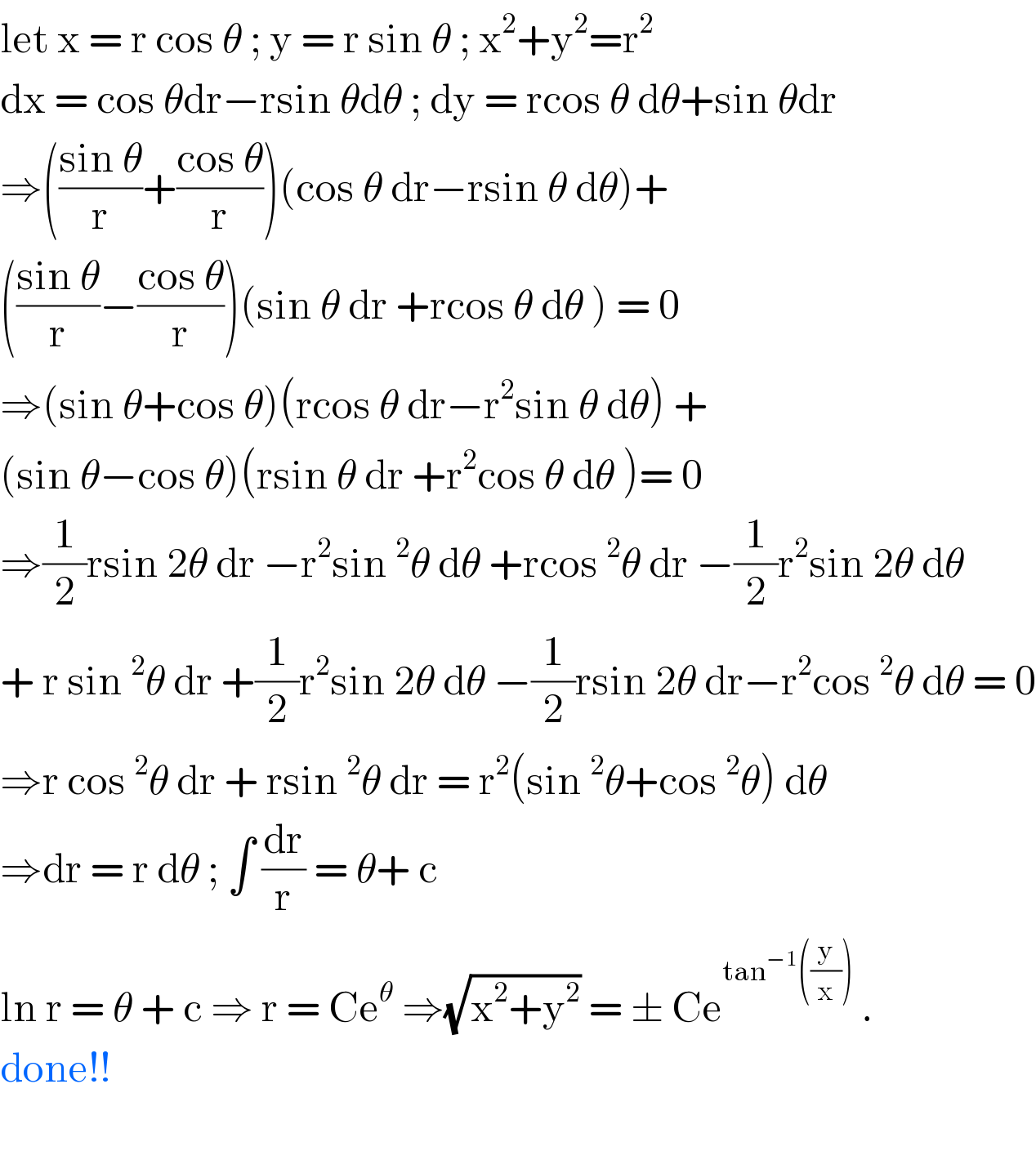
let x = r cos θ ; y = r sin θ ; x^2 +y^2 =r^2 dx = cos θdr−rsin θdθ ; dy = rcos θ dθ+sin θdr ⇒(((sin θ)/r)+((cos θ)/r))(cos θ dr−rsin θ dθ)+ (((sin θ)/r)−((cos θ)/r))(sin θ dr +rcos θ dθ ) = 0 ⇒(sin θ+cos θ)(rcos θ dr−r^2 sin θ dθ) + (sin θ−cos θ)(rsin θ dr +r^2 cos θ dθ )= 0 ⇒(1/2)rsin 2θ dr −r^2 sin^2 θ dθ +rcos^2 θ dr −(1/2)r^2 sin 2θ dθ + r sin^2 θ dr +(1/2)r^2 sin 2θ dθ −(1/2)rsin 2θ dr−r^2 cos^2 θ dθ = 0 ⇒r cos^2 θ dr + rsin^2 θ dr = r^2 (sin^2 θ+cos^2 θ) dθ ⇒dr = r dθ ; ∫ (dr/r) = θ+ c ln r = θ + c ⇒ r = Ce^θ ⇒(√(x^2 +y^2 )) = ± Ce^(tan^(−1) ((y/x))) . done!!
$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{r}\:\mathrm{cos}\:\theta\:;\:\mathrm{y}\:=\:\mathrm{r}\:\mathrm{sin}\:\theta\:;\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\mathrm{dx}\:=\:\mathrm{cos}\:\theta\mathrm{dr}−\mathrm{rsin}\:\theta\mathrm{d}\theta\:;\:\mathrm{dy}\:=\:\mathrm{rcos}\:\theta\:\mathrm{d}\theta+\mathrm{sin}\:\theta\mathrm{dr} \\ $$$$\Rightarrow\left(\frac{\mathrm{sin}\:\theta}{\mathrm{r}}+\frac{\mathrm{cos}\:\theta}{\mathrm{r}}\right)\left(\mathrm{cos}\:\theta\:\mathrm{dr}−\mathrm{rsin}\:\theta\:\mathrm{d}\theta\right)+ \\ $$$$\left(\frac{\mathrm{sin}\:\theta}{\mathrm{r}}−\frac{\mathrm{cos}\:\theta}{\mathrm{r}}\right)\left(\mathrm{sin}\:\theta\:\mathrm{dr}\:+\mathrm{rcos}\:\theta\:\mathrm{d}\theta\:\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\left(\mathrm{rcos}\:\theta\:\mathrm{dr}−\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:\theta\:\mathrm{d}\theta\right)\:+ \\ $$$$\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)\left(\mathrm{rsin}\:\theta\:\mathrm{dr}\:+\mathrm{r}^{\mathrm{2}} \mathrm{cos}\:\theta\:\mathrm{d}\theta\:\right)=\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{rsin}\:\mathrm{2}\theta\:\mathrm{dr}\:−\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{d}\theta\:+\mathrm{rcos}\:^{\mathrm{2}} \theta\:\mathrm{dr}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta\:\mathrm{d}\theta\: \\ $$$$+\:\mathrm{r}\:\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{dr}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta\:\mathrm{d}\theta\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{rsin}\:\mathrm{2}\theta\:\mathrm{dr}−\mathrm{r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{r}\:\mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{dr}\:+\:\mathrm{rsin}\:^{\mathrm{2}} \theta\:\mathrm{dr}\:=\:\mathrm{r}^{\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\right)\:\mathrm{d}\theta \\ $$$$\Rightarrow\mathrm{dr}\:=\:\mathrm{r}\:\mathrm{d}\theta\:;\:\int\:\frac{\mathrm{dr}}{\mathrm{r}}\:=\:\theta+\:\mathrm{c}\: \\ $$$$\mathrm{ln}\:\mathrm{r}\:=\:\theta\:+\:\mathrm{c}\:\Rightarrow\:\mathrm{r}\:=\:\mathrm{Ce}^{\theta} \:\Rightarrow\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:=\:\pm\:\mathrm{Ce}^{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{x}}\right)} \:. \\ $$$$\mathrm{done}!! \\ $$$$ \\ $$
Commented by i jagooll last updated on 23/May/20
waw..=great
$$\mathrm{waw}..=\mathrm{great} \\ $$$$ \\ $$
Commented by peter frank last updated on 23/May/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 23/May/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 23/May/20
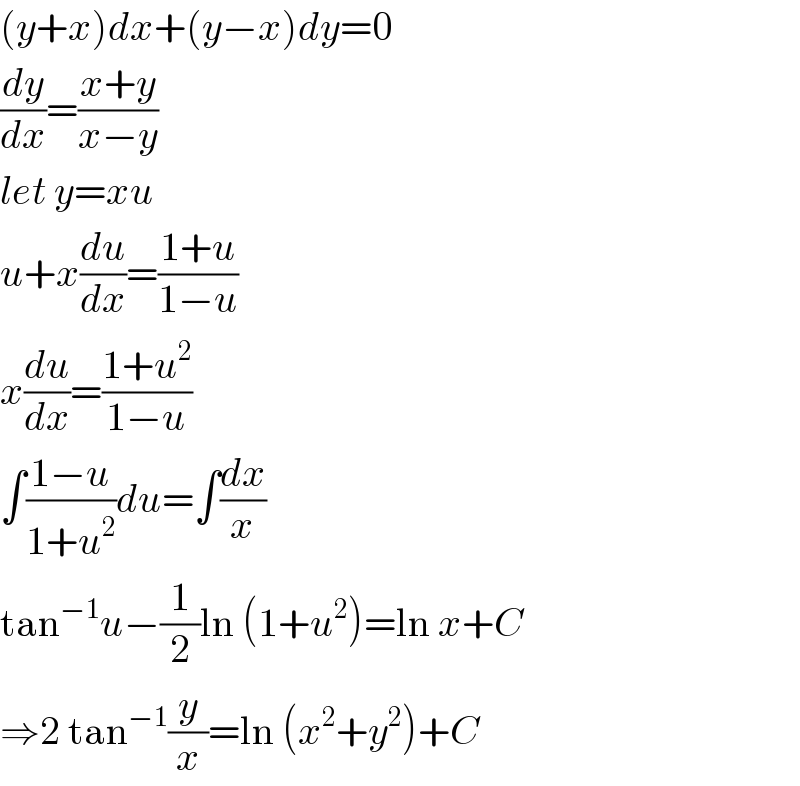
(y+x)dx+(y−x)dy=0 (dy/dx)=((x+y)/(x−y)) let y=xu u+x(du/dx)=((1+u)/(1−u)) x(du/dx)=((1+u^2 )/(1−u)) ∫((1−u)/(1+u^2 ))du=∫(dx/x) tan^(−1) u−(1/2)ln (1+u^2 )=ln x+C ⇒2 tan^(−1) (y/x)=ln (x^2 +y^2 )+C
$$\left({y}+{x}\right){dx}+\left({y}−{x}\right){dy}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}+{y}}{{x}−{y}} \\ $$$${let}\:{y}={xu} \\ $$$${u}+{x}\frac{{du}}{{dx}}=\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}} \\ $$$${x}\frac{{du}}{{dx}}=\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\mathrm{1}−{u}} \\ $$$$\int\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}=\int\frac{{dx}}{{x}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {u}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+{u}^{\mathrm{2}} \right)=\mathrm{ln}\:{x}+{C} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{{y}}{{x}}=\mathrm{ln}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *