Question Number 2735 by prakash jain last updated on 25/Nov/15
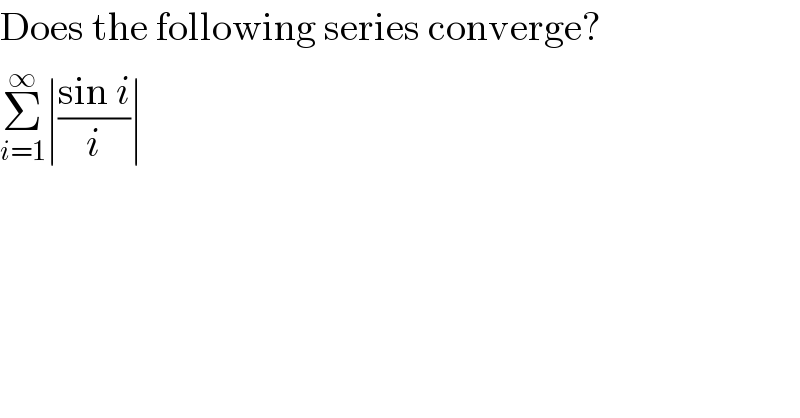
$$\mathrm{Does}\:\mathrm{the}\:\mathrm{following}\:\mathrm{series}\:\mathrm{converge}? \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\mid\frac{\mathrm{sin}\:{i}}{{i}}\mid \\ $$
Commented by Filup last updated on 26/Nov/15
![There is a limit lim_(x→∞) ∣((sin x)/x)∣=∣lim_(x→∞) ((sin x)/x)∣ sine is bound such that sin(x)∈[0, 1] =∣((0 to 1)/∞)∣=∣0∣=0 ∴There is a limit such that: lim_(x→∞) ∣((sin x)/x)∣=0](https://www.tinkutara.com/question/Q2741.png)
$$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{limit} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\mid\frac{\mathrm{sin}\:{x}}{{x}}\mid=\mid\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{{x}}\mid \\ $$$$\mathrm{sine}\:\mathrm{is}\:\mathrm{bound}\:\mathrm{such}\:\mathrm{that}\:\mathrm{sin}\left({x}\right)\in\left[\mathrm{0},\:\mathrm{1}\right] \\ $$$$=\mid\frac{\mathrm{0}\:\mathrm{to}\:\mathrm{1}}{\infty}\mid=\mid\mathrm{0}\mid=\mathrm{0} \\ $$$$ \\ $$$$\therefore\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{limit}\:\mathrm{such}\:\mathrm{that}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\mid\frac{\mathrm{sin}\:{x}}{{x}}\mid=\mathrm{0} \\ $$
Commented by Rasheed Soomro last updated on 26/Nov/15

$${Is}\:\frac{\mathrm{0}}{\infty}=\mathrm{0}?\:{Is}\:{this}\:{not}\:{indeterminte}\:{case}? \\ $$
Commented by Filup last updated on 26/Nov/15
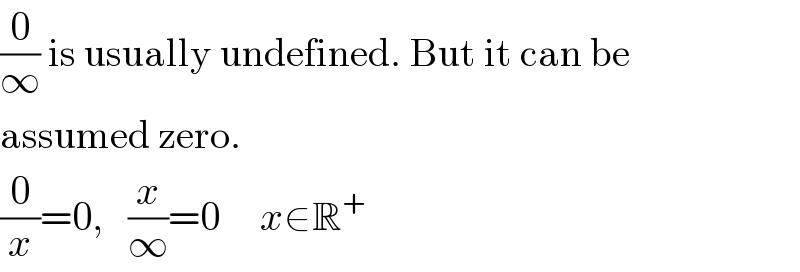
$$\frac{\mathrm{0}}{\infty}\:\mathrm{is}\:\mathrm{usually}\:\mathrm{undefined}.\:\mathrm{But}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{assumed}\:\mathrm{zero}. \\ $$$$\frac{\mathrm{0}}{{x}}=\mathrm{0},\:\:\:\frac{{x}}{\infty}=\mathrm{0}\:\:\:\:\:{x}\in\mathbb{R}^{+} \\ $$
Commented by prakash jain last updated on 26/Nov/15

$$\mathrm{0}/\infty\:\mathrm{is}\:\mathrm{not}\:\mathrm{indeterminate},\:\mathrm{it}\:\mathrm{is}\:\mathrm{0}. \\ $$$$\mathrm{Also}\:\mathrm{0}^{\infty} \:\mathrm{is}\:\mathrm{also}\:\mathrm{zero}. \\ $$$$\mathrm{Indeterminate}\:\mathrm{forms}\:\mathrm{are} \\ $$$$\mathrm{0}^{\mathrm{0}} ,\mathrm{0}\centerdot\infty,\:\frac{\infty}{\infty},\infty−\infty,\infty^{\mathrm{0}} ,\mathrm{1}^{\infty} ,\frac{\mathrm{0}}{\mathrm{0}} \\ $$
Commented by Filup last updated on 27/Nov/15

$${O}\mathrm{h}?\:\mathrm{Well}\:\mathrm{I}\:\mathrm{learnt}\:\mathrm{something}! \\ $$
Commented by Filup last updated on 27/Nov/15

$$\mathrm{Why}\:\mathrm{is}\:\infty^{\mathrm{0}} \:\mathrm{and}\:\mathrm{1}^{\infty} \:\mathrm{undefined}? \\ $$$$\mathrm{1}^{\mathrm{n}} =\mathrm{1}×\mathrm{1}×…×\mathrm{1}\:{n}\:\mathrm{times} \\ $$$$\mathrm{1}^{\infty} \:\mathrm{is}\:\mathrm{still}\:\mathrm{1}\:\mathrm{regardless},\:\mathrm{is}\:\mathrm{it}\:\mathrm{not}? \\ $$
Commented by RasheedAhmad last updated on 27/Nov/15
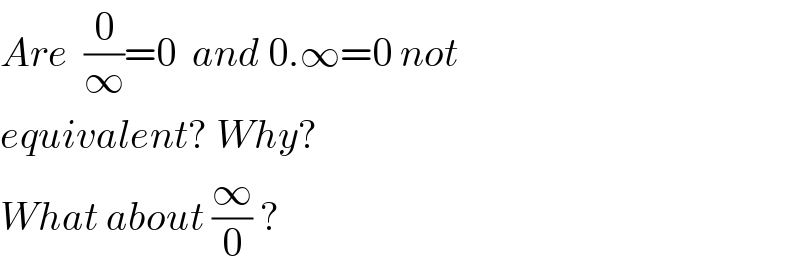
$${Are}\:\:\frac{\mathrm{0}}{\infty}=\mathrm{0}\:\:{and}\:\mathrm{0}.\infty=\mathrm{0}\:{not} \\ $$$${equivalent}?\:{Why}? \\ $$$${What}\:{about}\:\frac{\infty}{\mathrm{0}}\:? \\ $$
Commented by 123456 last updated on 27/Nov/15

$$\mathrm{1}^{\infty} \:\mathrm{is}\:\mathrm{undertemined}\:\mathrm{because}\:\mathrm{its}\:\mathrm{depends} \\ $$$$\mathrm{of}\:\mathrm{function} \\ $$$$\mathrm{A}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} ={e}\: \\ $$$$\mathrm{B}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/{x}} =\mathrm{1} \\ $$$$\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{limits}\:\mathrm{of}\:\mathrm{1}^{\infty} \:\mathrm{but}\:\mathrm{take} \\ $$$$\mathrm{differents}\:\mathrm{value} \\ $$$$\mathrm{same}\:\mathrm{to}\:\infty^{\mathrm{0}} \\ $$$$\mathrm{C}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{x}^{\mathrm{1}/{x}} =\mathrm{1} \\ $$$$\mathrm{D}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left({x}^{{x}} \right)^{\mathrm{1}/{x}} =+\infty \\ $$
Answered by Filup last updated on 26/Nov/15
![for ∣sin i∣ as i→∞, it is a repetition of the sum of values between [0, 1] The sum can be evaluated as: Σ_(i=1) ^∞ ((∣sin i∣)/i) ∵i>0, ∴∣i∣=i for (a/b)=c, For a∈[0, +∞), as b→∞, c→0 For i∈[1, +∞), ∣sin i∣∈(0, 1)=c Σ_(i=1) ^∞ c(1/i)=c×∞ Harmonic sequence More correctly: Σ_(i=1) ^∞ ∣((sin i)/i)∣=Σ_(i=1) ^∞ ((0 to 1)/i)=cΣ_(i=1) ^∞ (1/i) =c×∞ Does not converge](https://www.tinkutara.com/question/Q2739.png)
$${for}\:\mid\mathrm{sin}\:{i}\mid\:\mathrm{as}\:{i}\rightarrow\infty, \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{repetition}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{values} \\ $$$$\mathrm{between}\:\left[\mathrm{0},\:\mathrm{1}\right] \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{sum}\:\mathrm{can}\:\mathrm{be}\:\mathrm{evaluated}\:\mathrm{as}: \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mid\mathrm{sin}\:{i}\mid}{{i}}\:\:\:\:\:\:\:\:\:\because{i}>\mathrm{0},\:\therefore\mid{i}\mid={i} \\ $$$$ \\ $$$$\mathrm{for}\:\frac{{a}}{{b}}={c},\:\:\:\mathrm{For}\:{a}\in\left[\mathrm{0},\:+\infty\right),\:\mathrm{as}\:{b}\rightarrow\infty,\:\:{c}\rightarrow\mathrm{0} \\ $$$$\mathrm{For}\:{i}\in\left[\mathrm{1},\:+\infty\right),\:\mid\mathrm{sin}\:{i}\mid\in\left(\mathrm{0},\:\mathrm{1}\right)={c} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{c}\frac{\mathrm{1}}{{i}}={c}×\infty\:\:\mathrm{Harmonic}\:\mathrm{sequence} \\ $$$${More}\:{correctly}: \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\mid\frac{\mathrm{sin}\:{i}}{{i}}\mid=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{0}\:\mathrm{to}\:\mathrm{1}}{{i}}={c}\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$$={c}×\infty \\ $$$${Does}\:{not}\:{converge} \\ $$
Commented by Filup last updated on 26/Nov/15

$$\mathrm{The}\:\mathrm{proof}\:\mathrm{above}\:\mathrm{is}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{informal}, \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{do}\:\mathrm{believe}\:\mathrm{the}\:\mathrm{concept}\:\mathrm{is}\:\mathrm{correct}. \\ $$
Commented by prakash jain last updated on 26/Nov/15
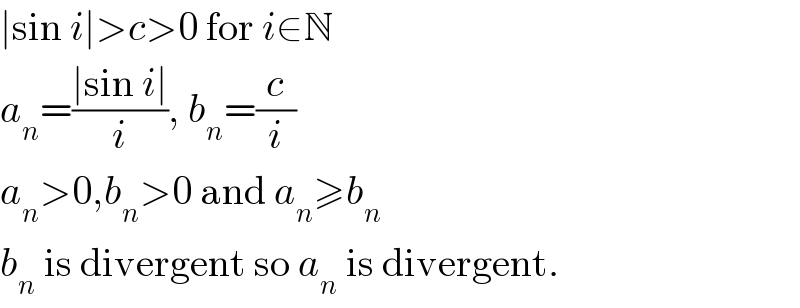
$$\mid\mathrm{sin}\:{i}\mid>{c}>\mathrm{0}\:\mathrm{for}\:{i}\in\mathbb{N} \\ $$$${a}_{{n}} =\frac{\mid\mathrm{sin}\:{i}\mid}{{i}},\:{b}_{{n}} =\frac{{c}}{{i}} \\ $$$${a}_{{n}} >\mathrm{0},{b}_{{n}} >\mathrm{0}\:\mathrm{and}\:{a}_{{n}} \geqslant{b}_{{n}} \\ $$$${b}_{{n}} \:\mathrm{is}\:\mathrm{divergent}\:\mathrm{so}\:{a}_{{n}} \:\mathrm{is}\:\mathrm{divergent}. \\ $$
