Menu Close

Prove-that-if-Li-2-x-n-1-x-n-n-2-then-x-Li-2-x-Li-2-1-x-pi-2-6-ln-x-ln-1-x-x-0-1-Li-2-x-Li-2-1-x-pi-2-6-ln-x-2-Find-A-n-1-n-n-2-an

Tinku Tara 0 Comments
Pin




Question Number 68270 by ~ À ® @ 237 ~ last updated on 08/Sep/19
Prove that if Li_2 (x)=Σ_(n=1) (x^n /n^2 ) then ∀ x Li_2 (x)+Li_2 (1−x) = (π^2 /6) −ln(x)ln(1−x) ∀ x∉[0:1] Li_2 (x)+Li_2 ((1/x)) = −(π^2 /6) −[ln(−x)]^2 Find A=Σ_(n=1) ^∞ (ϕ^n /n^2 ) and B=Σ_(n=1) ^∞ (2^n /n^2 )
$$\:{Prove}\:{that}\:\:{if}\:\:{Li}_{\mathrm{2}} \left({x}\right)=\underset{{n}=\mathrm{1}} {\sum}\:\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }\:\:\:{then} \\ $$$$\forall\:{x}\:\:{Li}_{\mathrm{2}} \left({x}\right)+{Li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right)\:\: \\ $$$$\forall\:{x}\notin\left[\mathrm{0}:\mathrm{1}\right]\:{Li}_{\mathrm{2}} \left({x}\right)+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}\right)\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\left[{ln}\left(−{x}\right)\right]^{\mathrm{2}} \:\: \\ $$$${Find}\:\:{A}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\varphi^{{n}} }{{n}^{\mathrm{2}} }\:\:{and}\:\:{B}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}^{{n}} }{{n}^{\mathrm{2}} }\:\: \\ $$
Commented by mathmax by abdo last updated on 10/Sep/19
let f(x)=l_i^2 (x)+l_i_2 (1−x) and g(x)=(π^2 /6)−ln(x)ln(1−x) with ∣x∣<1 we havef^′ (x)=l_i_2 ^′ (x)−l_i_2 ′(1−x) but l^′ i_2 (x) =Σ_(n=1) ^∞ (x^(n−1) /n) =(1/x)Σ_(n=1) ^∞ (x^n /n) =−(1/x)ln(1−x) and l_i_2 ^′ (1−x) =(1/(1−x))ln(x) ⇒f^′ (x)=−(1/x)ln(1−x)+(1/(1−x))lnx g^′ (x) =−(1/x)ln(1−x)−(ln(x)((−1)/(1−x)))=−(1/x)ln(1−x) +(1/(1−x))ln(x) ⇒f(x)=g(x)+c lim_(x→1) f(x) =L_i_2 (1)+L_i_2 (0) =Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /6) ⇒c=0 lim_(x→1) g(x) =(π^2 /6) −lim_(x→1) ln(x)ln(1−x) 1−x=t ⇒lim_(x→1) ln(x)ln(1−x)=lim_(t→0) ln(1−t)lnt =lim_(t→0) t ln(t) ((ln(1−t))/t) =0 ⇒c =0 ⇒ L_i_2 (x)+L_i_2 (1−x)=−ln(x)ln(1−x) perhaps tbere is a error in the question...!
$${let}\:{f}\left({x}\right)={l}_{{i}^{\mathrm{2}} } \left({x}\right)+{l}_{{i}_{\mathrm{2}} } \:\left(\mathrm{1}−{x}\right)\:\:{and}\:{g}\left({x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right) \\ $$$${with}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{havef}^{'} \left({x}\right)={l}_{{i}_{\mathrm{2}} } ^{'} \left({x}\right)−{l}_{{i}_{\mathrm{2}} } '\left(\mathrm{1}−{x}\right)\:{but}\:{l}^{'} {i}_{\mathrm{2}} \left({x}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}−\mathrm{1}} }{{n}}\:=\frac{\mathrm{1}}{{x}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:=−\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}−{x}\right)\:{and} \\ $$$${l}_{{i}_{\mathrm{2}} } ^{'} \left(\mathrm{1}−{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}−{x}}{ln}\left({x}\right)\:\Rightarrow{f}^{'} \left({x}\right)=−\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}−{x}\right)+\frac{\mathrm{1}}{\mathrm{1}−{x}}{lnx} \\ $$$${g}^{'} \left({x}\right)\:=−\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}−{x}\right)−\left({ln}\left({x}\right)\frac{−\mathrm{1}}{\mathrm{1}−{x}}\right)=−\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}−{x}\right)\:+\frac{\mathrm{1}}{\mathrm{1}−{x}}{ln}\left({x}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={g}\left({x}\right)+{c}\: \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {f}\left({x}\right)\:={L}_{{i}_{\mathrm{2}} } \left(\mathrm{1}\right)+{L}_{{i}_{\mathrm{2}} } \:\left(\mathrm{0}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow{c}=\mathrm{0}\: \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {g}\left({x}\right)\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−{lim}_{{x}\rightarrow\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right) \\ $$$$\mathrm{1}−{x}={t}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right)={lim}_{{t}\rightarrow\mathrm{0}} {ln}\left(\mathrm{1}−{t}\right){lnt} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:{t}\:{ln}\left({t}\right)\:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}\:=\mathrm{0}\:\Rightarrow{c}\:=\mathrm{0}\:\Rightarrow \\ $$$${L}_{{i}_{\mathrm{2}} } \left({x}\right)+{L}_{{i}_{\mathrm{2}} } \left(\mathrm{1}−{x}\right)=−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right) \\ $$$${perhaps}\:{tbere}\:{is}\:{a}\:{error}\:{in}\:{the}\:{question}…! \\ $$$$ \\ $$
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
Thanks for this sir but there is none error
$${Thanks}\:{for}\:{this}\:{sir}\:{but}\:{there}\:{is}\:{none}\:{error} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
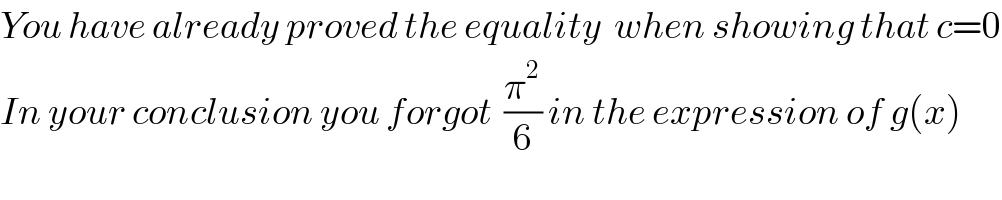
You have already proved the equality when showing that c=0 In your conclusion you forgot (π^2 /6) in the expression of g(x)
$${You}\:{have}\:{already}\:{proved}\:{the}\:{equality}\:\:{when}\:{showing}\:{that}\:{c}=\mathrm{0} \\ $$$${In}\:{your}\:{conclusion}\:{you}\:{forgot}\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:{in}\:{the}\:{expression}\:{of}\:{g}\left({x}\right) \\ $$
Answered by mind is power last updated on 09/Sep/19
are you sur for li_2 (x)+li_2 ((1/x))=−(π^2 /6_ )−[ln(−x)]^2 ...
$${are}\:{you}\:{sur}\:\:{for}\:{li}_{\mathrm{2}} \left({x}\right)+{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}_{} }−\left[{ln}\left(−{x}\right)\right]^{\mathrm{2}} … \\ $$
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
I forget something here sir: Sorry It is Li_2 (x)+Li_2 ((1/x))=−_ (π^2 /6) −(1/2)[ln(−x)]^2
$$\:{I}\:{forget}\:\:{something}\:{here}\:{sir}:\:{Sorry}\: \\ $$$${It}\:{is}\:\:\:{Li}_{\mathrm{2}} \left({x}\right)+{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}\right)=−_{} \frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(−{x}\right)\right]^{\mathrm{2}} \: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *