Question Number 95198 by Fikret last updated on 23/May/20
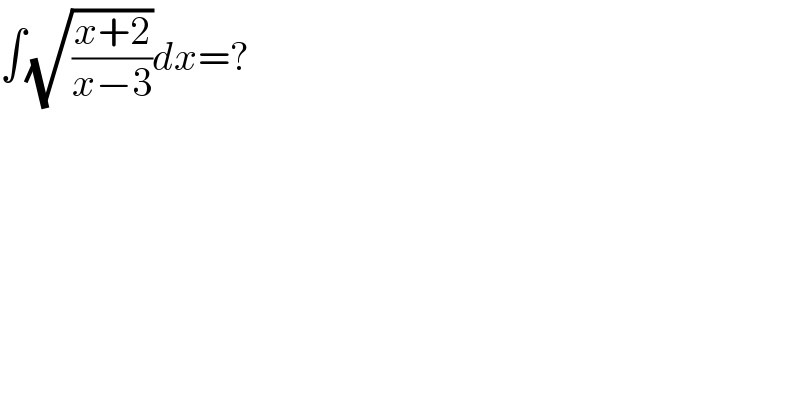
$$\int\sqrt{\frac{{x}+\mathrm{2}}{{x}−\mathrm{3}}}{dx}=? \\ $$
Answered by MJS last updated on 23/May/20
![∫(√((x+2)/(x−3)))dx= [t=(√((x+2)/(x−3))) → dx=−(2/5)(√((x−3)^3 (x+2)))] =−10∫(t^2 /((t^2 −1)^2 ))dt= =−(5/2)(∫(dt/((t−1)^2 ))+∫(dt/((t+1)^2 ))+∫(dt/(t−1))−∫(dt/(t+1)))= =(5/2)((1/(t−1))+(1/(t+1))−ln (t−1) +ln (t+1))= =(5/(t^2 −1))+(5/2)ln ((t+1)/(t−1)) = =(√((x−3)(x+2)))+(5/2)ln (2x−1+2(√((x−3)(x+2)))) +C](https://www.tinkutara.com/question/Q95207.png)
$$\int\sqrt{\frac{{x}+\mathrm{2}}{{x}−\mathrm{3}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{{x}+\mathrm{2}}{{x}−\mathrm{3}}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)}\right] \\ $$$$=−\mathrm{10}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$=−\frac{\mathrm{5}}{\mathrm{2}}\left(\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }+\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }+\int\frac{{dt}}{{t}−\mathrm{1}}−\int\frac{{dt}}{{t}+\mathrm{1}}\right)= \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}+\frac{\mathrm{1}}{{t}+\mathrm{1}}−\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\mathrm{ln}\:\left({t}+\mathrm{1}\right)\right)= \\ $$$$=\frac{\mathrm{5}}{{t}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\:= \\ $$$$=\sqrt{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{2}\right)}+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}{x}−\mathrm{1}+\mathrm{2}\sqrt{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{2}\right)}\right)\:+{C} \\ $$
