Question Number 95222 by bobhans last updated on 24/May/20
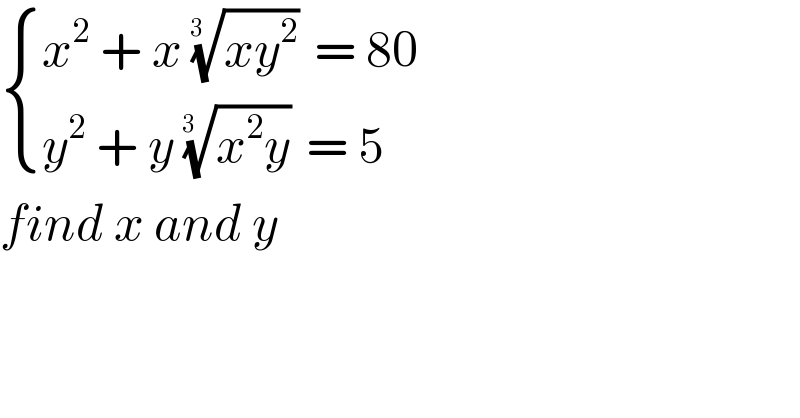
$$\begin{cases}{{x}^{\mathrm{2}} \:+\:{x}\:\sqrt[{\mathrm{3}\:\:}]{{xy}^{\mathrm{2}} }\:=\:\mathrm{80}\:}\\{{y}^{\mathrm{2}} \:+\:{y}\:\sqrt[{\mathrm{3}\:\:}]{{x}^{\mathrm{2}} {y}}\:=\:\mathrm{5}\:}\end{cases} \\ $$$${find}\:{x}\:{and}\:{y}\: \\ $$
Answered by john santu last updated on 24/May/20

$$\mathrm{set}\:\sqrt[{\mathrm{3}\:\:}]{{x}}\:=\:{p}\:\&\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{y}}\:=\:{q} \\ $$$$\begin{cases}{{p}^{\mathrm{6}} \:+\:{p}^{\mathrm{4}} {q}^{\mathrm{2}} \:=\:\mathrm{80}}\\{{q}^{\mathrm{6}} \:+\:{p}^{\mathrm{2}} {q}^{\mathrm{4}} \:=\:\mathrm{5}\:}\end{cases} \\ $$$$\begin{cases}{{p}^{\mathrm{4}} \:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\:=\:\mathrm{80}}\\{{q}^{\mathrm{4}} \:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\:=\:\mathrm{5}\:}\end{cases} \\ $$$$\frac{{p}^{\mathrm{4}} }{{q}^{\mathrm{4}} }\:=\:\mathrm{16}\:\Rightarrow\:{p}\:=\:\pm\:\mathrm{2}{q}\: \\ $$$$\Rightarrow\mathrm{16}{q}^{\mathrm{4}} \:\left(\mathrm{4}{q}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\:=\:\mathrm{80} \\ $$$$\mathrm{80}{q}^{\mathrm{4}} \:=\:\mathrm{80}\:\Rightarrow{q}\:=\:\pm\:\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:{p}\:=\:\pm\:\mathrm{2}\: \\ $$$$\begin{cases}{\sqrt[{\mathrm{3}\:\:}]{{x}}\:=\:\pm\:\mathrm{3}\:\Rightarrow{x}\:=\:\pm\:\mathrm{8}}\\{\sqrt[{\mathrm{3}\:\:}]{{y}}\:=\:\pm\:\mathrm{1}\:\Rightarrow\:\mathrm{y}\:=\:\pm\:\mathrm{1}}\end{cases} \\ $$$$\mathrm{solution}\:\left\{\left(−\mathrm{8},−\mathrm{1}\right),\left(\mathrm{8},\mathrm{1}\right)\:\right\} \\ $$
Commented by bobhans last updated on 24/May/20

$$\mathrm{waww}…\mathrm{great} \\ $$
