Question Number 133829 by metamorfose last updated on 24/Feb/21
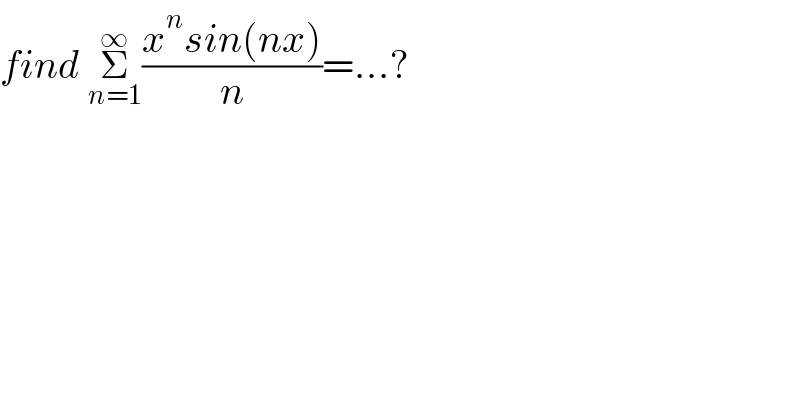
$${find}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} {sin}\left({nx}\right)}{{n}}=…? \\ $$
Answered by Dwaipayan Shikari last updated on 24/Feb/21

$${log}\left(\mathrm{1}−{xe}^{{ix}} \right)={log}\left(\sqrt{\left(\mathrm{1}−{xcosx}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}\right)+{itan}^{−\mathrm{1}} \frac{{xsinx}}{{xcosx}−\mathrm{1}} \\ $$$$−{i}\left({xsin}\left({x}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}{sin}\left(\mathrm{3}{x}\right)+…\right)={itan}^{−\mathrm{1}} \frac{{xsinx}}{{xcosx}−\mathrm{1}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} {sin}\left({nx}\right)}{{n}}=−{tan}^{−\mathrm{1}} \frac{{xsinx}}{{xcosx}−\mathrm{1}} \\ $$
