Menu Close

find-the-angle-of-plane-2x-y-2z-1-and-x-3y-2z-2-

Tinku Tara 0 Comments
Pin




Question Number 95509 by i jagooll last updated on 25/May/20
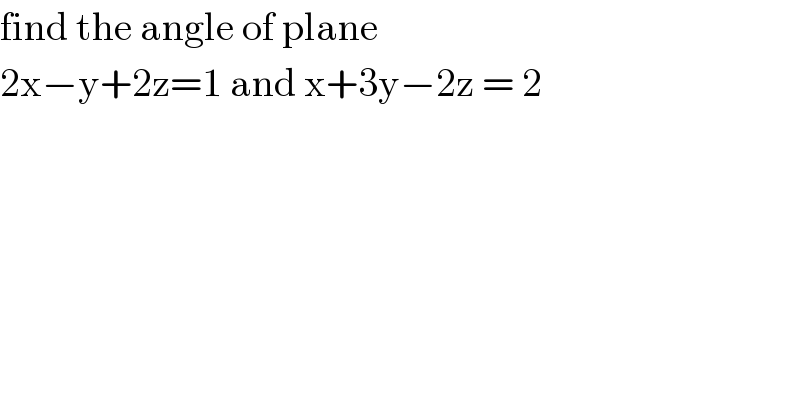
find the angle of plane 2x−y+2z=1 and x+3y−2z = 2
$$\mathrm{find}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{plane} \\ $$$$\mathrm{2x}−\mathrm{y}+\mathrm{2z}=\mathrm{1}\:\mathrm{and}\:\mathrm{x}+\mathrm{3y}−\mathrm{2z}\:=\:\mathrm{2} \\ $$
Answered by bobhans last updated on 25/May/20
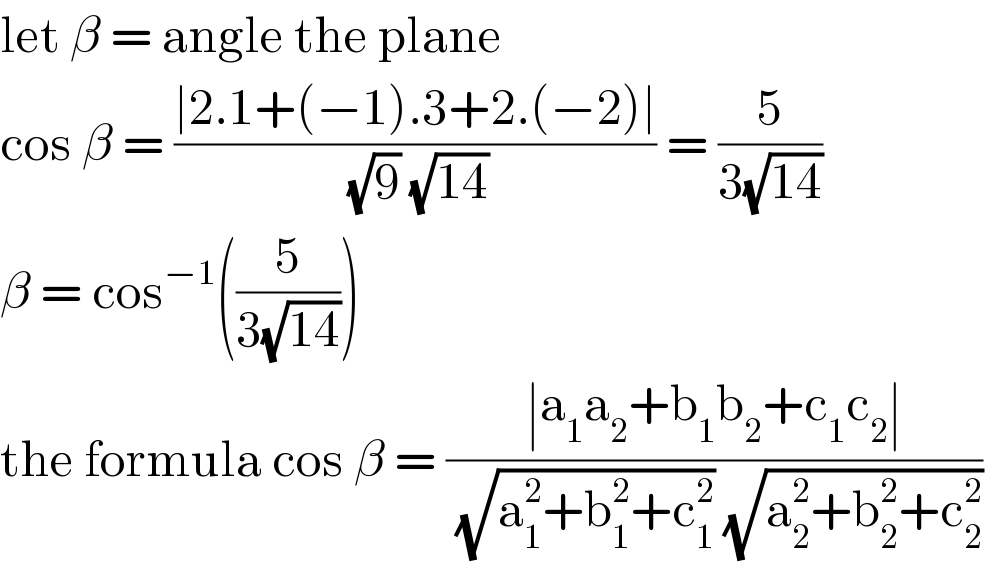
let β = angle the plane cos β = ((∣2.1+(−1).3+2.(−2)∣)/( (√9) (√(14)))) = (5/(3(√(14)))) β = cos^(−1) ((5/(3(√(14))))) the formula cos β = ((∣a_1 a_2 +b_1 b_2 +c_1 c_2 ∣)/( (√(a_1 ^2 +b_1 ^2 +c_1 ^2 )) (√(a_2 ^2 +b_2 ^2 +c_2 ^2 ))))
$$\mathrm{let}\:\beta\:=\:\mathrm{angle}\:\mathrm{the}\:\mathrm{plane}\: \\ $$$$\mathrm{cos}\:\beta\:=\:\frac{\mid\mathrm{2}.\mathrm{1}+\left(−\mathrm{1}\right).\mathrm{3}+\mathrm{2}.\left(−\mathrm{2}\right)\mid}{\:\sqrt{\mathrm{9}}\:\sqrt{\mathrm{14}}}\:=\:\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{14}}} \\ $$$$\beta\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{14}}}\right)\: \\ $$$$\mathrm{the}\:\mathrm{formula}\:\mathrm{cos}\:\beta\:=\:\frac{\mid\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} \mathrm{b}_{\mathrm{2}} +\mathrm{c}_{\mathrm{1}} \mathrm{c}_{\mathrm{2}} \mid}{\:\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{c}_{\mathrm{1}} ^{\mathrm{2}} }\:\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{c}_{\mathrm{2}} ^{\mathrm{2}} }}\: \\ $$
Answered by mr W last updated on 25/May/20
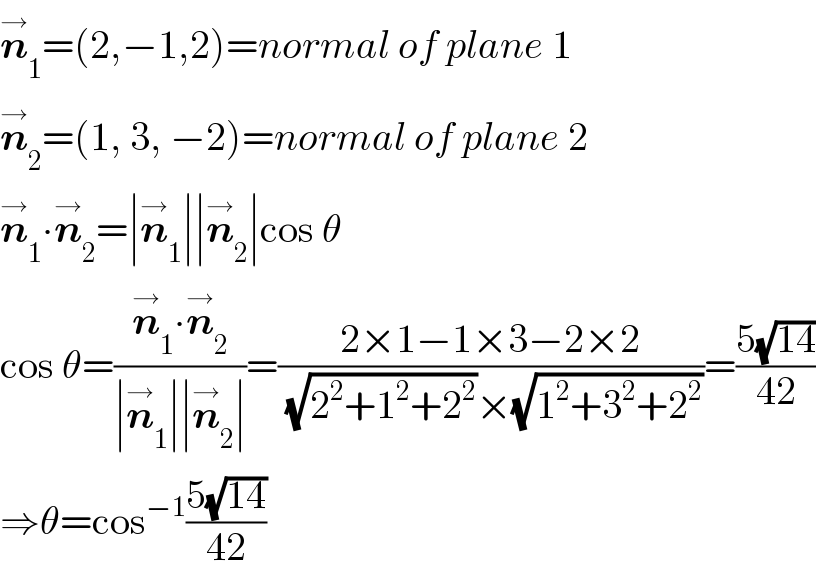
n_1 ^→ =(2,−1,2)=normal of plane 1 n_2 ^→ =(1, 3, −2)=normal of plane 2 n_1 ^→ ∙n_2 ^→ =∣n_1 ^→ ∣∣n_2 ^→ ∣cos θ cos θ=((n_1 ^→ ∙n_2 ^→ )/(∣n_1 ^→ ∣∣n_2 ^→ ∣))=((2×1−1×3−2×2)/( (√(2^2 +1^2 +2^2 ))×(√(1^2 +3^2 +2^2 ))))=((5(√(14)))/(42)) ⇒θ=cos^(−1) ((5(√(14)))/(42))
$$\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{1}} =\left(\mathrm{2},−\mathrm{1},\mathrm{2}\right)={normal}\:{of}\:{plane}\:\mathrm{1} \\ $$$$\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{2}} =\left(\mathrm{1},\:\mathrm{3},\:−\mathrm{2}\right)={normal}\:{of}\:{plane}\:\mathrm{2} \\ $$$$\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{1}} \centerdot\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{2}} =\mid\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{1}} \mid\mid\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{2}} \mid\mathrm{cos}\:\theta \\ $$$$\mathrm{cos}\:\theta=\frac{\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{1}} \centerdot\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{2}} }{\mid\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{1}} \mid\mid\overset{\rightarrow} {\boldsymbol{{n}}}_{\mathrm{2}} \mid}=\frac{\mathrm{2}×\mathrm{1}−\mathrm{1}×\mathrm{3}−\mathrm{2}×\mathrm{2}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }×\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{5}\sqrt{\mathrm{14}}}{\mathrm{42}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{14}}}{\mathrm{42}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *