Question Number 68308 by mr W last updated on 08/Sep/19
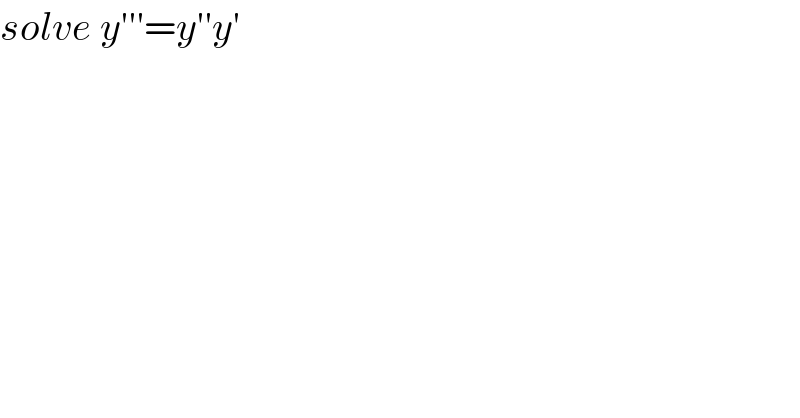
$${solve}\:{y}'''={y}''{y}' \\ $$
Answered by mind is power last updated on 08/Sep/19
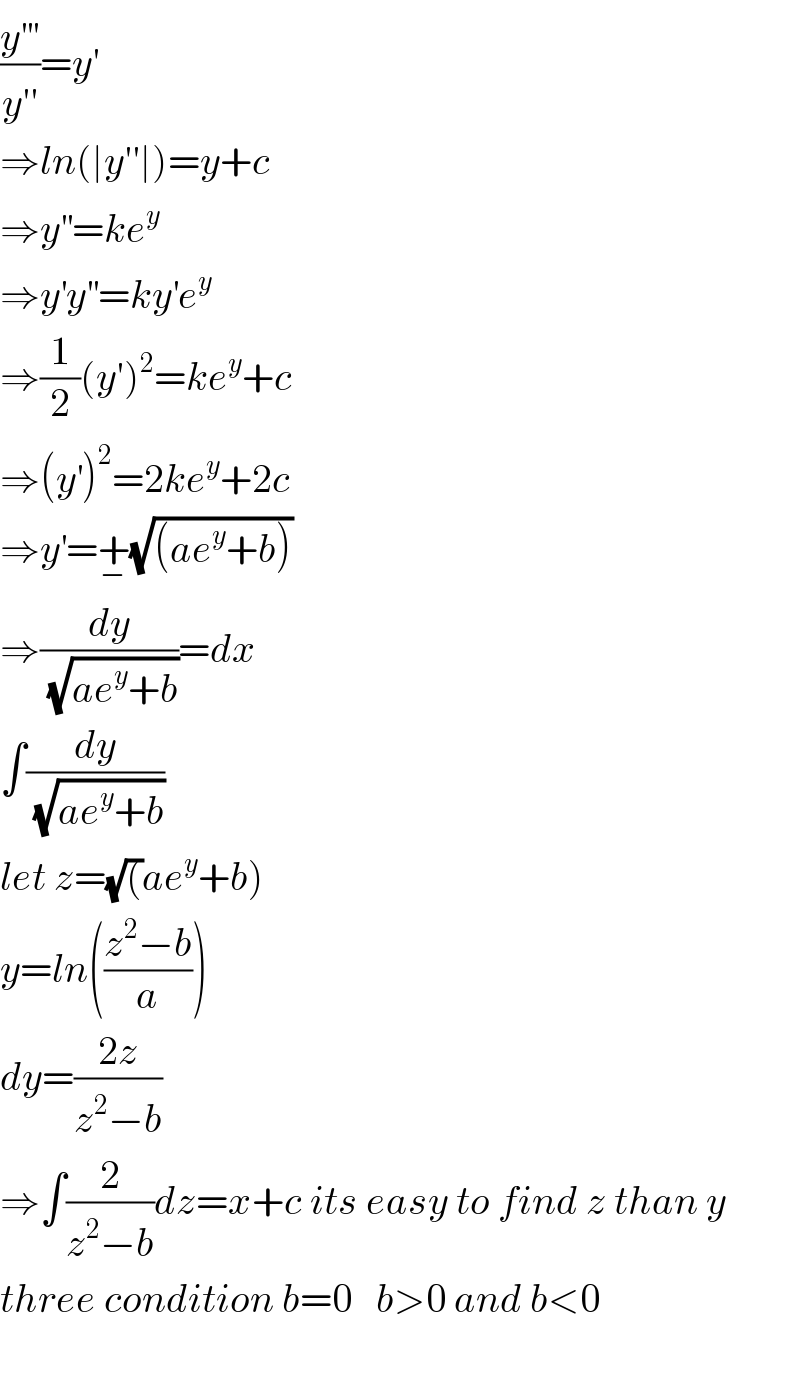
$$\frac{{y}^{'''} }{{y}'^{'} }={y}' \\ $$$$\Rightarrow{ln}\left(\mid{y}''\mid\right)={y}+{c} \\ $$$$\Rightarrow{y}^{''} ={ke}^{{y}} \\ $$$$\Rightarrow{y}^{'} {y}^{''} ={ky}^{'} {e}^{{y}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left({y}'\right)^{\mathrm{2}} ={ke}^{{y}} +{c} \\ $$$$\Rightarrow\left({y}^{'} \right)^{\mathrm{2}} =\mathrm{2}{ke}^{{y}} +\mathrm{2}{c} \\ $$$$\Rightarrow{y}^{'} =\underset{−} {+}\sqrt{\left({ae}^{{y}} +{b}\right)} \\ $$$$\Rightarrow\frac{{dy}}{\:\sqrt{{ae}^{{y}} +{b}}}={dx} \\ $$$$\int\frac{{dy}}{\:\sqrt{{ae}^{{y}} +{b}}} \\ $$$$\left.{let}\:{z}=\sqrt{\left(\right.}{ae}^{{y}} +{b}\right) \\ $$$${y}={ln}\left(\frac{{z}^{\mathrm{2}} −{b}}{{a}}\right) \\ $$$${dy}=\frac{\mathrm{2}{z}}{{z}^{\mathrm{2}} −{b}} \\ $$$$\Rightarrow\int\frac{\mathrm{2}}{{z}^{\mathrm{2}} −{b}}{dz}={x}+{c}\:{its}\:{easy}\:{to}\:{find}\:{z}\:{than}\:{y} \\ $$$${three}\:{condition}\:{b}=\mathrm{0}\:\:\:{b}>\mathrm{0}\:{and}\:{b}<\mathrm{0} \\ $$$$ \\ $$
