Question Number 29983 by abdo imad last updated on 14/Feb/18
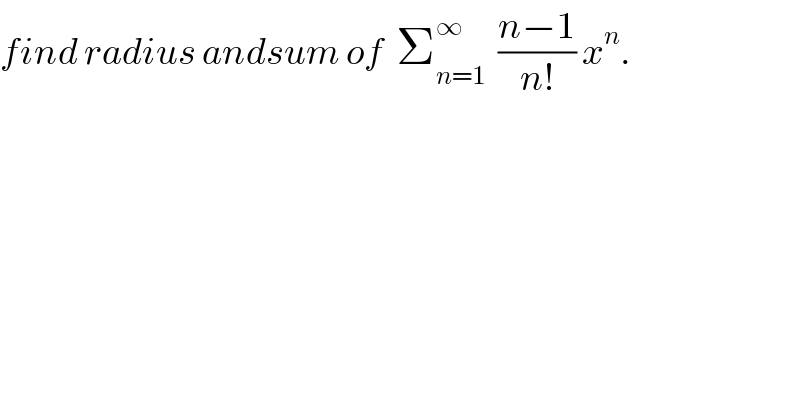
$${find}\:{radius}\:{andsum}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{n}−\mathrm{1}}{{n}!}\:{x}^{{n}} . \\ $$
Commented by abdo imad last updated on 15/Feb/18
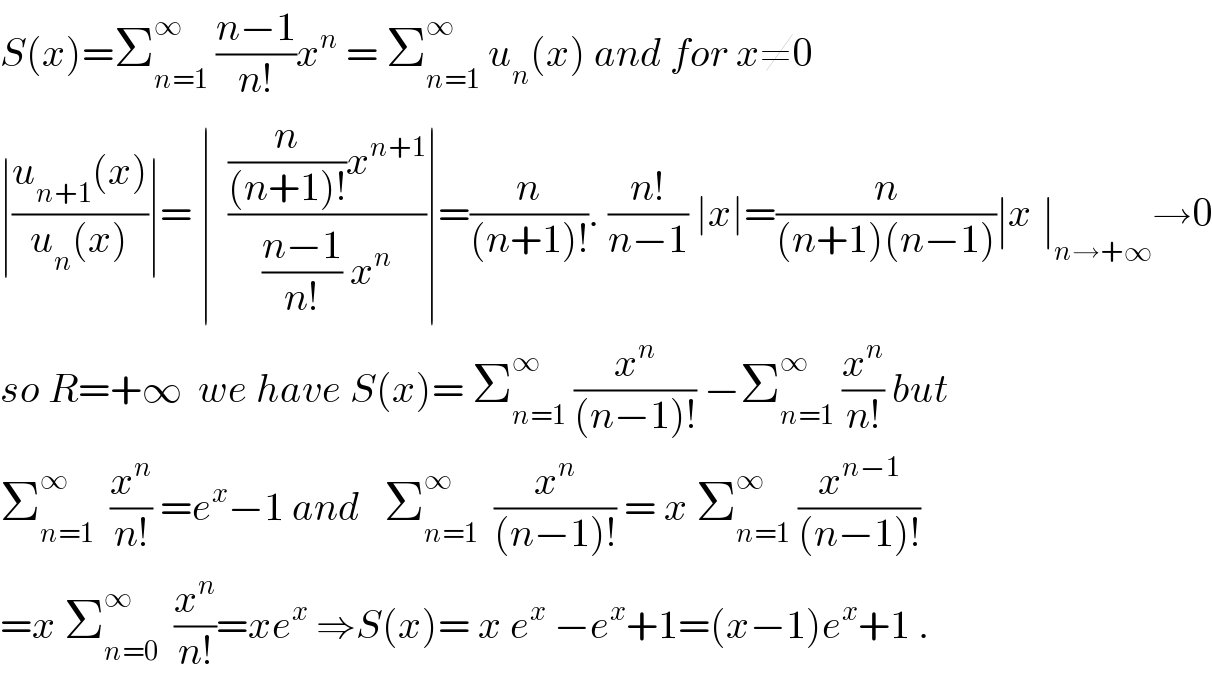
$${S}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}−\mathrm{1}}{{n}!}{x}^{{n}} \:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{u}_{{n}} \left({x}\right)\:{and}\:{for}\:{x}\neq\mathrm{0} \\ $$$$\mid\frac{{u}_{{n}+\mathrm{1}} \left({x}\right)}{{u}_{{n}} \left({x}\right)}\mid=\:\mid\:\:\frac{\frac{{n}}{\left({n}+\mathrm{1}\right)!}{x}^{{n}+\mathrm{1}} }{\frac{{n}−\mathrm{1}}{{n}!}\:{x}^{{n}} }\mid=\frac{{n}}{\left({n}+\mathrm{1}\right)!}.\:\frac{{n}!}{{n}−\mathrm{1}}\:\mid{x}\mid=\frac{{n}}{\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)}\mid{x}_{} \mid_{{n}\rightarrow+\infty} \rightarrow\mathrm{0} \\ $$$${so}\:{R}=+\infty\:\:{we}\:{have}\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{\left({n}−\mathrm{1}\right)!}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}!}\:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}!}\:={e}^{{x}} −\mathrm{1}\:{and}\:\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{\left({n}−\mathrm{1}\right)!}\:=\:{x}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}−\mathrm{1}} }{\left({n}−\mathrm{1}\right)!} \\ $$$$={x}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}!}={xe}^{{x}} \:\Rightarrow{S}\left({x}\right)=\:{x}\:{e}^{{x}} \:−{e}^{{x}} +\mathrm{1}=\left({x}−\mathrm{1}\right){e}^{{x}} +\mathrm{1}\:. \\ $$
