Question Number 161089 by mnjuly1970 last updated on 12/Dec/21
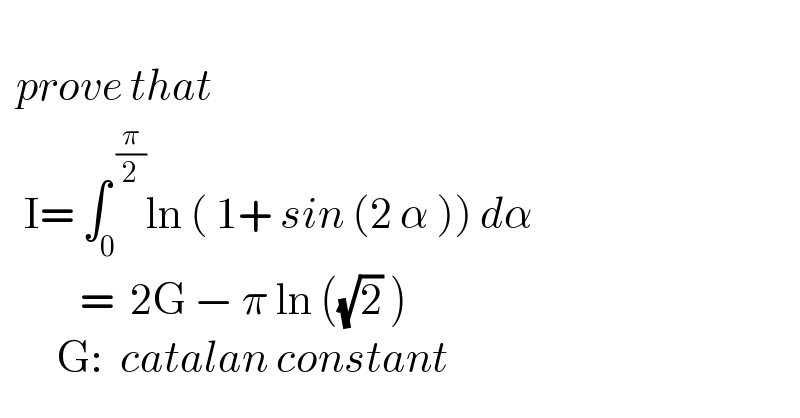
$$ \\ $$$$\:\:{prove}\:{that} \\ $$$$\:\:\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\:\left(\:\mathrm{1}+\:{sin}\:\left(\mathrm{2}\:\alpha\:\right)\right)\:{d}\alpha\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{2G}\:−\:\pi\:\mathrm{ln}\:\left(\sqrt{\mathrm{2}}\:\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{G}:\:\:{catalan}\:{constant} \\ $$
Answered by Ar Brandon last updated on 11/Dec/21
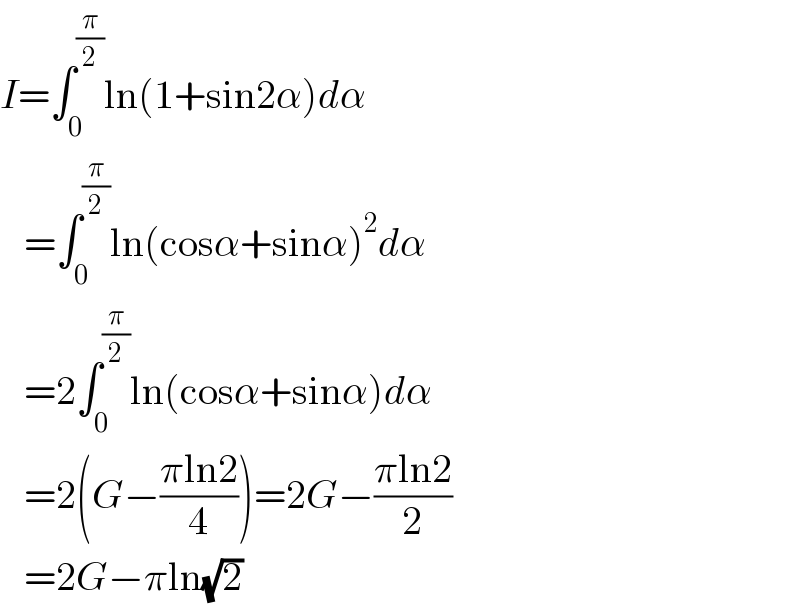
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{sin2}\alpha\right){d}\alpha \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}\alpha+\mathrm{sin}\alpha\right)^{\mathrm{2}} {d}\alpha \\ $$$$\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}\alpha+\mathrm{sin}\alpha\right){d}\alpha \\ $$$$\:\:\:=\mathrm{2}\left({G}−\frac{\pi\mathrm{ln2}}{\mathrm{4}}\right)=\mathrm{2}{G}−\frac{\pi\mathrm{ln2}}{\mathrm{2}} \\ $$$$\:\:\:=\mathrm{2}{G}−\pi\mathrm{ln}\sqrt{\mathrm{2}} \\ $$
Answered by mnjuly1970 last updated on 12/Dec/21

Commented by Tawa11 last updated on 12/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 12/Dec/21

