Question Number 95578 by i jagooll last updated on 26/May/20
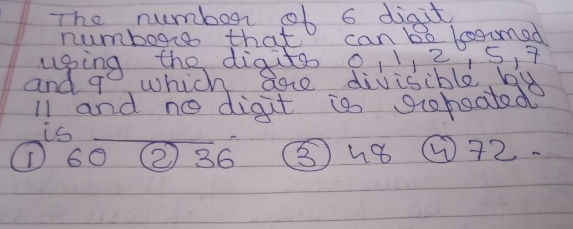
Commented by i jagooll last updated on 26/May/20
anyone can help?
Commented by john santu last updated on 26/May/20

$$\mathrm{60} \\ $$
Commented by john santu last updated on 26/May/20
We can write the six digit number as a1a2a3a4a5a6 . Since 10≡−1(mod11) and 100≡1(mod11) , the overall condition that the number be divisible by 11 may be expressed as a1+a3+a5≡a2+a4+a6(mod11) . Since we are given that a1+a2+a3+a4+a5+a6=0+1+2+5+7+9=24≡2(mod11) , it follows that a1+a3+a5≡a2+a4+a6≡1(mod11) . The only feasible solutions will therefore have a1+a3+a5=a2+a4+a6=12 . A little bit of trial and error will show that the two sets {a1,a3,a5} and {a2,a4,a6} must be {0,5,7} and {1,2,9} , not necessarily
respectively. The assignment of the sets can be done in 2 ways and then the digits can be permuted in 3!∗3!=36 ways giving a total of 72 numbers satisfying the required properties. Of those, 12 will have a leading digit of zero meaning they aren’t really six digit numbers. This gives 60 six digit numbers satisfying the required properties.
Commented by mr W last updated on 26/May/20
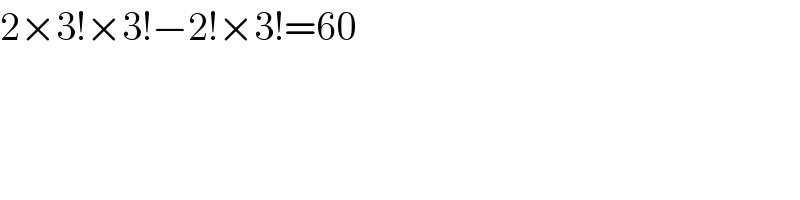
$$\mathrm{2}×\mathrm{3}!×\mathrm{3}!−\mathrm{2}!×\mathrm{3}!=\mathrm{60} \\ $$
Commented by john santu last updated on 26/May/20

$$\mathrm{explain} \\ $$
Commented by mr W last updated on 26/May/20

$${we}\:{divide}\:{the}\:\mathrm{6}\:{digits}\:{into}\:{two}\:{groups}: \\ $$$${group}\:{A}\:{with}\:\mathrm{0},\mathrm{5},\mathrm{7} \\ $$$${group}\:{B}\:{with}\:\mathrm{1},\mathrm{2},\mathrm{9} \\ $$$${both}\:{groups}\:{have}\:{the}\:{same}\:{sum}, \\ $$$${namly}\:\mathrm{12}. \\ $$$${numbers}\:{in}\:{form}\:{of}\:{ABABAB}\:{or} \\ $$$${BABABA}\:{are}\:{divisible}\:{by}\:\mathrm{11},\:{since} \\ $$$$\Sigma{A}−\Sigma{B}=\mathrm{0}\:{which}\:{is}\:{divisible}\:{by}\:\mathrm{11}. \\ $$$$ \\ $$$${number}\:{of}\:{numbers}\:{in}\:{form}\:{BABABA} \\ $$$${is}\:\mathrm{3}!×\mathrm{3}!. \\ $$$$ \\ $$$${number}\:{of}\:{numbers}\:{in}\:{form}\:{ABABAB} \\ $$$${is}\:\mathrm{3}!×\mathrm{3}!,\:{but}\:{some}\:{of}\:{them}\:{begin}\:{with} \\ $$$$“\mathrm{0}''\:{which}\:{are}\:{invalid}.\:{number}\:{of} \\ $$$${invalid}\:{numbers}\:{is}\:\mathrm{2}!×\mathrm{3}!. \\ $$$$ \\ $$$${therefore}\:{the}\:{number}\:{of}\:{valid} \\ $$$${numbers}\:{is}:\:\mathrm{2}×\mathrm{3}!×\mathrm{3}!−\mathrm{2}!×\mathrm{3}!=\mathrm{60}. \\ $$$$ \\ $$$${we}\:{have}\:{no}\:{other}\:{possibilty}\:{to}\:{divide} \\ $$$${the}\:\mathrm{6}\:{given}\:{digits}\:{into}\:{two}\:{groups}\: \\ $$$${with}\:{the}\:{same}\:{sum}\:{or}\:{with}\:{sums} \\ $$$${with}\:{the}\:{difference}\:\mathrm{11},\:\mathrm{22}\:{etc}. \\ $$
Commented by mr W last updated on 26/May/20
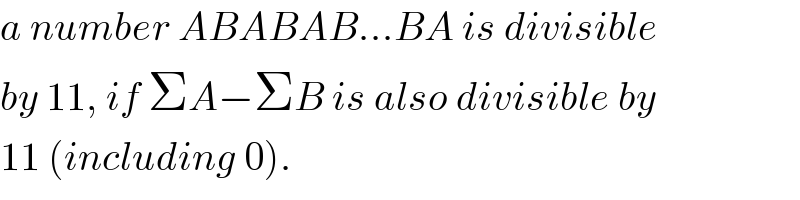
$${a}\:{number}\:{ABABAB}…{BA}\:{is}\:{divisible} \\ $$$${by}\:\mathrm{11},\:{if}\:\Sigma{A}−\Sigma{B}\:{is}\:{also}\:{divisible}\:{by} \\ $$$$\mathrm{11}\:\left({including}\:\mathrm{0}\right). \\ $$
Commented by i jagooll last updated on 26/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
