Question Number 161136 by mnjuly1970 last updated on 12/Dec/21
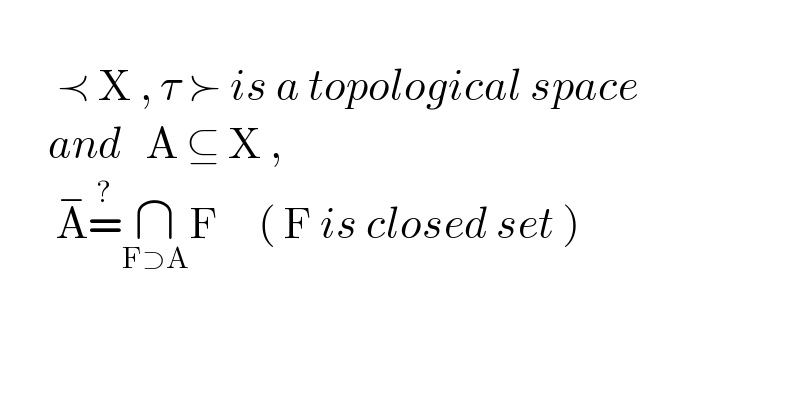
$$ \\ $$$$\:\:\:\:\:\:\:\prec\:\mathrm{X}\:,\:\tau\:\succ\:{is}\:{a}\:{topological}\:{space} \\ $$$$\:\:\:\:\:\:{and}\:\:\:\mathrm{A}\:\subseteq\:\mathrm{X}\:, \\ $$$$\:\:\:\:\:\:\:\overset{−} {\mathrm{A}}\overset{?} {=}\underset{\mathrm{F}\supset\mathrm{A}} {\cap}\mathrm{F}\:\:\:\:\:\left(\:\mathrm{F}\:{is}\:{closed}\:{set}\:\right) \\ $$$$ \\ $$
Answered by mindispower last updated on 12/Dec/21

$${A}\subset{F}\:,{not}\:{empty}\:{set}\:\overset{−} {{A}}\in\left\{{A}\subset{F},{F}\:{is}\:{closed}\:{set}\right\} \\ $$$${A}\in\underset{{A}\subset{F}} {\cap}{F}\Rightarrow\overset{−} {{A}}\in{closed}\left(\underset{{A}\subset{F}} {\cap}{F}\right)=\underset{{A}\subset{F}} {\cap}{F} \\ $$$$\overset{−} {{F}}={F}\:\:\:{since}\:{F}\:{is}\:{closed} \\ $$$$\left(\mathrm{2}\right)\:{A}\subset{F}\:\:,{now}\:{lets}\:{used}\:{that}\:\overset{−} {{A}}\:{is}\:{the}\:{smallest} \\ $$$${closed}\:{set}\:{that}\:{contient}\:{A} \\ $$$${A}\subset\overset{−} {{A}},\:\:\underset{{A}\subset{F}} {\cap}{F}=\overset{−} {{A}}\cap\:\:\left(\underset{{A}\subset{F}−\left\{\overset{−} {{A}}\right\}} {\cap}{F}\right)\subset\overset{−} {{A}}…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:{nd}\:\left(\mathrm{2}\right)\Rightarrow\overset{−} {{A}}=\underset{{A}\subset{F}} {\cap}{F} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 13/Dec/21
$$\:\:\:{great}\:{sir}\:{power}\:\:{bravo}… \\ $$
Answered by mindispower last updated on 12/Dec/21

$${more}/{quation}\:{like}\:{this}\:{sir}\:{please} \\ $$$${morphisum}\:{modular}\:{Groups} \\ $$$$ \\ $$
