Question Number 161178 by amin96 last updated on 13/Dec/21
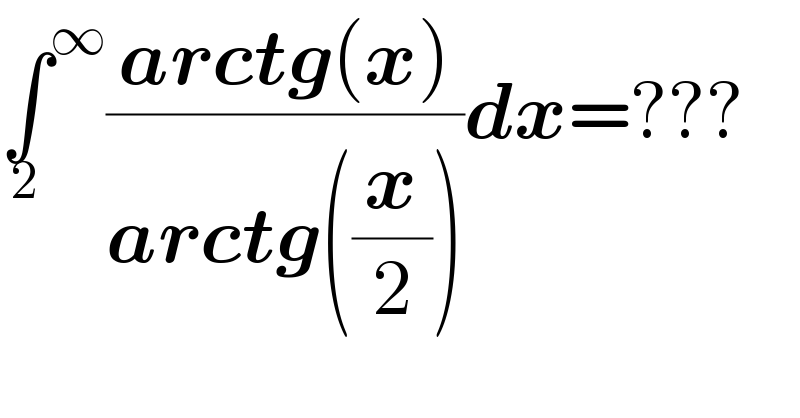
$$\underset{\mathrm{2}} {\int}^{\infty} \frac{\boldsymbol{{arctg}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{arctg}}\left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}\boldsymbol{{dx}}=??? \\ $$
Answered by MJS_new last updated on 13/Dec/21
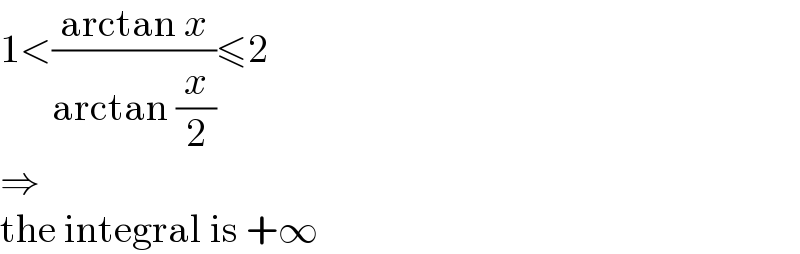
$$\mathrm{1}<\frac{\mathrm{arctan}\:{x}}{\mathrm{arctan}\:\frac{{x}}{\mathrm{2}}}\leqslant\mathrm{2} \\ $$$$\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{is}\:+\infty \\ $$
