Question-161186

Question Number 161186 by mathlove last updated on 13/Dec/21

Answered by Rasheed.Sindhi last updated on 13/Dec/21

lim_(x→∞) ((((√2) x+10)/( (√2) x−11)))^((2x−1)/(x+1)) =lim_(x→∞) (((x((√2) +((10)/x)))/( x((√2) −((11)/x)))))^((x(2−(1/x)))/(x(1+(1/x)))) =lim_(x→∞) ((((√2) +((10)/x))/( (√2) −((11)/x))))^((2−(1/x))/(1+(1/x))) = ((((√2) +0)/( (√2) −0)))^((2−0)/(1+0)) =1^2 =1

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\sqrt{\mathrm{2}}\:{x}+\mathrm{10}}{\:\sqrt{\mathrm{2}}\:{x}−\mathrm{11}}\right)^{\frac{\mathrm{2}{x}−\mathrm{1}}{{x}+\mathrm{1}}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\cancel{{x}}\left(\sqrt{\mathrm{2}}\:+\frac{\mathrm{10}}{{x}}\right)}{\:\cancel{{x}}\left(\sqrt{\mathrm{2}}\:−\frac{\mathrm{11}}{{x}}\right)}\right)^{\frac{\cancel{{x}}\left(\mathrm{2}−\frac{\mathrm{1}}{{x}}\right)}{\cancel{{x}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\sqrt{\mathrm{2}}\:+\frac{\mathrm{10}}{{x}}}{\:\sqrt{\mathrm{2}}\:−\frac{\mathrm{11}}{{x}}}\right)^{\frac{\mathrm{2}−\frac{\mathrm{1}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}} \\ $$$$=\:\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{0}}{\:\sqrt{\mathrm{2}}\:−\mathrm{0}}\right)^{\frac{\mathrm{2}−\mathrm{0}}{\mathrm{1}+\mathrm{0}}} \\ $$$$=\mathrm{1}^{\mathrm{2}} =\mathrm{1} \\ $$

Answered by qaz last updated on 13/Dec/21

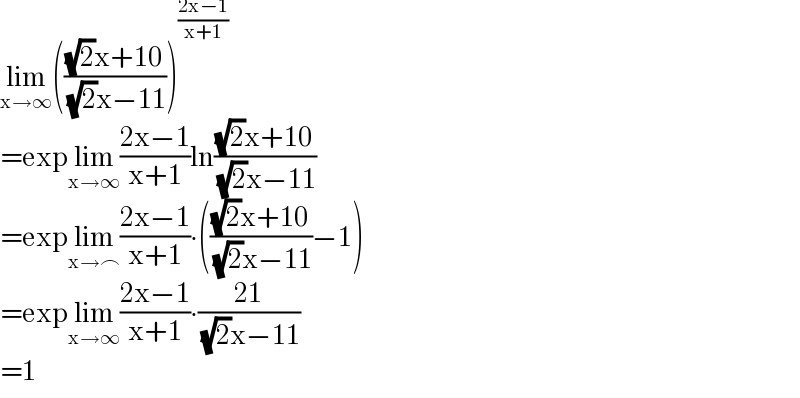
lim_(x→∞) ((((√2)x+10)/( (√2)x−11)))^((2x−1)/(x+1)) =explim_(x→∞) ((2x−1)/(x+1))ln(((√2)x+10)/( (√2)x−11)) =explim_(x→⌢) ((2x−1)/(x+1))∙((((√2)x+10)/( (√2)x−11))−1) =explim_(x→∞) ((2x−1)/(x+1))∙((21)/( (√2)x−11)) =1

$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{10}}{\:\sqrt{\mathrm{2}}\mathrm{x}−\mathrm{11}}\right)^{\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$$$=\mathrm{exp}\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mathrm{ln}\frac{\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{10}}{\:\sqrt{\mathrm{2}}\mathrm{x}−\mathrm{11}} \\ $$$$=\mathrm{exp}\underset{\mathrm{x}\rightarrow\frown} {\mathrm{lim}}\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\centerdot\left(\frac{\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{10}}{\:\sqrt{\mathrm{2}}\mathrm{x}−\mathrm{11}}−\mathrm{1}\right) \\ $$$$=\mathrm{exp}\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\centerdot\frac{\mathrm{21}}{\:\sqrt{\mathrm{2}}\mathrm{x}−\mathrm{11}} \\ $$$$=\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply