Question Number 30165 by rahul 19 last updated on 17/Feb/18

Commented by ajfour last updated on 19/Feb/18

$${let}\:{us}\:{first}\:{choose}\:{a}\:{fixed}\:{x}-{axis}. \\ $$$$\bar {\omega}\:=\:\omega\hat {{k}}\:\:\:{and}\:{at}\:{time}\:{t}\:\:\theta=\omega{t} \\ $$$$\bar {{r}}={r}\left(\mathrm{cos}\:\theta\hat {{i}}+\mathrm{sin}\:\theta\hat {{j}}\right) \\ $$$$\:\:={r}\left(\mathrm{cos}\:\omega{t}\hat {{i}}+\mathrm{sin}\:\omega{t}\hat {{j}}\right)={r}\hat {{e}}_{{r}} \\ $$$$\bar {{v}}=\frac{{dr}}{{dt}}\hat {{e}}_{{r}} +\omega{r}\left(−\mathrm{sin}\:\omega{t}\hat {{i}}+\mathrm{cos}\:\omega{t}\hat {{j}}\right) \\ $$$$\:\:=\frac{{dr}}{{dt}}\hat {{e}}_{{r}} +\omega{r}\hat {{e}}_{\theta} \\ $$$$\bar {{a}}=\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }\hat {{e}}_{{r}} +\omega\frac{{dr}}{{dt}}\hat {{e}}_{\theta} +\omega\frac{{dr}}{{dt}}\hat {{e}}_{\theta} −\omega^{\mathrm{2}} {r}\hat {{e}}_{{r}} \\ $$$${as}\:{there}\:{is}\:{complete}\:{absence}\:{of} \\ $$$${force}\:{along}\:{radial}\:{direction},\:{so} \\ $$$${radial}\:{component}\:{of}\:{acceleration} \\ $$$${is}\:{zero}. \\ $$$$\Rightarrow\:\:\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }−\omega^{\mathrm{2}} {r}\:=\mathrm{0} \\ $$$$\:\:\:\:{let}\:\:{v}_{{r}} =\:\frac{{dr}}{{dt}} \\ $$$$\Rightarrow\:\:\frac{{v}_{{r}} {dv}_{{r}} }{{dr}}\:=\:\omega^{\mathrm{2}} {r} \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\:{v}_{{r}} } {v}_{{r}} {dr}\:=\:\omega^{\mathrm{2}} \int_{{R}/\mathrm{2}} ^{\:\:{r}} {rdr} \\ $$$$\:\:\:\:\:{v}_{{r}} ^{\mathrm{2}} \:=\:\omega^{\mathrm{2}} \left({r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${v}_{{r}} =\:\frac{{dr}}{{dt}}\:=\:\omega\sqrt{{r}^{\mathrm{2}} −\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\int_{{R}/\mathrm{2}} ^{\:\:{r}} \frac{{dr}}{\:\sqrt{{r}^{\mathrm{2}} −\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:=\:\omega\int_{\mathrm{0}} ^{\:\:{t}} {dt} \\ $$$$\Rightarrow\:\:\mathrm{ln}\:\left({r}+\sqrt{{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}}\right)\mid_{{R}/\mathrm{2}} ^{{r}} =\:\omega{t} \\ $$$$\Rightarrow\:\:{r}+\sqrt{{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}}\:=\:\frac{{R}}{\mathrm{2}}{e}^{\omega{t}} \:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:\:\:{rationalising}\:{and}\:{taking} \\ $$$${reciprocal}\:{we}\:{also}\:{get}, \\ $$$$\:\:\:\:\:\:{r}−\sqrt{{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}}\:=\:\frac{{R}}{\mathrm{2}}{e}^{−\omega{t}} \:\:\:\:…\left({ii}\right) \\ $$$${hence}\:{by}\:{adding}\:\left({i}\right)\:{and}\:\left({ii}\right) \\ $$$$\:\:\:\:\:\:\boldsymbol{{r}}\:=\:\frac{\boldsymbol{{R}}}{\mathrm{4}}\left(\boldsymbol{{e}}^{\boldsymbol{\omega{t}}} +\boldsymbol{{e}}^{−\boldsymbol{\omega{t}}} \right)\:\:. \\ $$$${Force}\:\left({tangential}\right)\:{on}\:{block}\:{by} \\ $$$${disc}\:\:\:=\:\bar {{F}}\:=\:{m}\left(\mathrm{2}\omega\frac{{dr}}{{dt}}\right)\hat {{e}}_{\theta} \\ $$$$\:\:\:\:\:\:\:\:\bar {{F}}\:=\mathrm{2}{m}\omega{v}_{{r}} \hat {{e}}_{\theta} \: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2}{m}\omega^{\mathrm{2}} \sqrt{{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}}\:\right)\hat {{e}}_{\theta} \\ $$$$\left({i}\right)−\left({ii}\right)\:{gives} \\ $$$$\:\:\:\:\:\:\sqrt{{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{4}}}\:=\frac{{R}}{\mathrm{4}}\left({e}^{\omega{t}} −{e}^{−\omega{t}} \right) \\ $$$$\:\:{hence}\:\:\bar {{F}}\:=\:\frac{{m}\omega^{\mathrm{2}} {R}}{\mathrm{2}}\left({e}^{\omega{t}} −{e}^{−\omega{t}} \right)\hat {{e}}_{\theta} \\ $$$${and}\:{if}\:{x}\:{axis}\:{is}\:{chosen}\:{to}\:{be} \\ $$$${along}\:{radial}\:{direction}\:{rotating} \\ $$$${along}\:{with}\:{disc}\:{then}\:\hat {{i}}\:{is}\:{along}\:\hat {{e}}_{{r}} \\ $$$${and}\:\:\hat {{j}}\:{is}\:{along}\:\hat {{e}}_{\theta} \:. \\ $$$${Then}\:\bar {{F}}\:=\:\frac{{m}\omega^{\mathrm{2}} {R}}{\mathrm{2}}\left({e}^{\omega{t}} −{e}^{−\omega{t}} \right)\hat {{j}} \\ $$$${disc}\:{also}\:{supports}\:{weight}\:{of}\:{block} \\ $$$${hence}\:{we}\:{also}\:{have}\:{a}\:{force} \\ $$$$\:\:{N}_{{z}} ={mg}\hat {{k}} \\ $$$$\bar {\boldsymbol{{N}}}\:\:{the}\:{reaction}\:{force}\:{of}\:{disc}\:{on} \\ $$$${block}\:{is}\:\:\:\bar {{N}}\:=\:\bar {{F}}+{mg}\hat {{k}} \\ $$$$\:\bar {{N}}\:=\:\frac{{m}\omega^{\mathrm{2}} {R}}{\mathrm{2}}\left({e}^{\omega{t}} −{e}^{\omega{t}} \right)\hat {{j}}+{mg}\hat {{k}}\:\:. \\ $$
Commented by ajfour last updated on 19/Feb/18
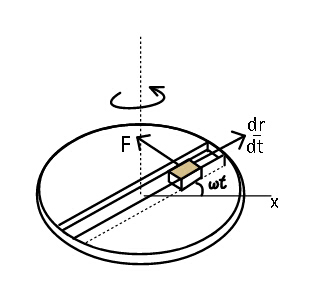
Commented by rahul 19 last updated on 19/Feb/18

$$\mathscr{W}\mathfrak{O}\mathscr{W}\:\ldots! \\ $$
