Menu Close

let-u-n-k-1-n-1-k-n-2-1-verify-that-x-x-2-2-ln-1-x-x-2-prove-that-u-n-is-convergente-and-find-its-limit-

Tinku Tara 0 Comments
Pin




Question Number 30173 by abdo imad last updated on 18/Feb/18
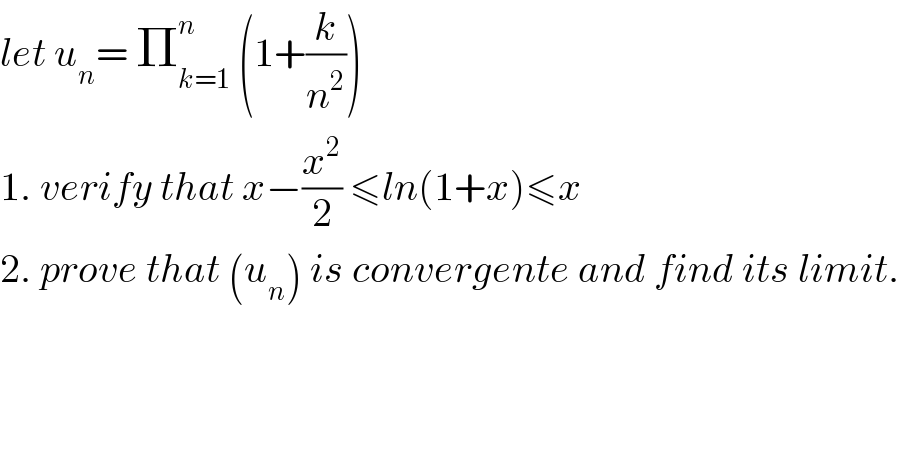
let u_n = Π_(k=1) ^n (1+(k/n^2 )) 1. verify that x−(x^2 /2) ≤ln(1+x)≤x 2. prove that (u_n ) is convergente and find its limit.
$${let}\:{u}_{{n}} =\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{1}.\:{verify}\:{that}\:{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$$\mathrm{2}.\:{prove}\:{that}\:\left({u}_{{n}} \right)\:{is}\:{convergente}\:{and}\:{find}\:{its}\:{limit}. \\ $$
Commented by abdo imad last updated on 21/Feb/18
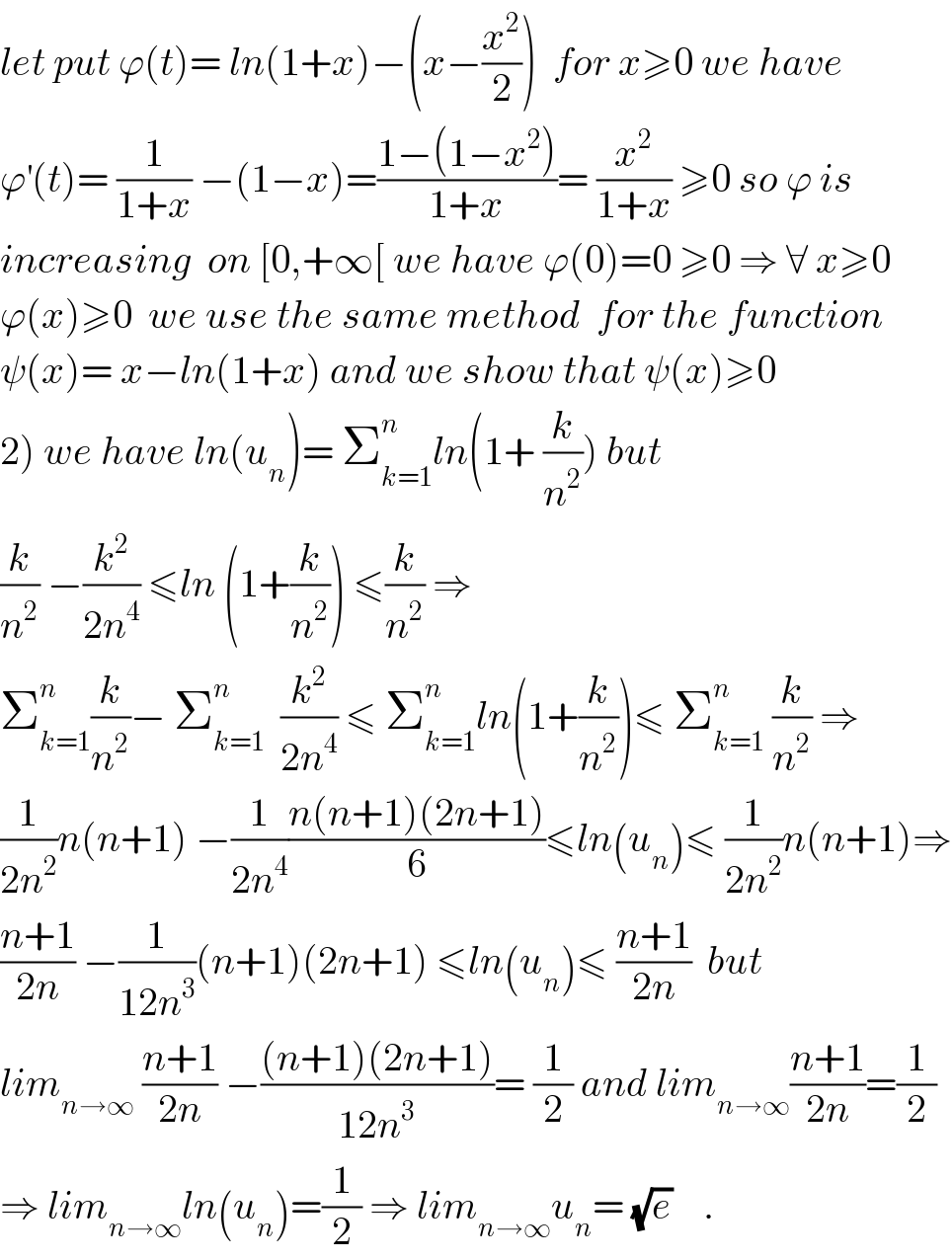
let put ϕ(t)= ln(1+x)−(x−(x^2 /2)) for x≥0 we have ϕ^′ (t)= (1/(1+x)) −(1−x)=((1−(1−x^2 ))/(1+x))= (x^2 /(1+x)) ≥0 so ϕ is increasing on [0,+∞[ we have ϕ(0)=0 ≥0 ⇒ ∀ x≥0 ϕ(x)≥0 we use the same method for the function ψ(x)= x−ln(1+x) and we show that ψ(x)≥0 2) we have ln(u_n )= Σ_(k=1) ^n ln(1+ (k/n^2 )) but (k/n^2 ) −(k^2 /(2n^4 )) ≤ln (1+(k/n^2 )) ≤(k/n^2 ) ⇒ Σ_(k=1) ^n (k/n^2 )− Σ_(k=1) ^n (k^2 /(2n^4 )) ≤ Σ_(k=1) ^n ln(1+(k/n^2 ))≤ Σ_(k=1) ^n (k/n^2 ) ⇒ (1/(2n^2 ))n(n+1) −(1/(2n^4 ))((n(n+1)(2n+1))/6)≤ln(u_n )≤ (1/(2n^2 ))n(n+1)⇒ ((n+1)/(2n)) −(1/(12n^3 ))(n+1)(2n+1) ≤ln(u_n )≤ ((n+1)/(2n)) but lim_(n→∞) ((n+1)/(2n)) −(((n+1)(2n+1))/(12n^3 ))= (1/2) and lim_(n→∞) ((n+1)/(2n))=(1/2) ⇒ lim_(n→∞) ln(u_n )=(1/2) ⇒ lim_(n→∞) u_n = (√e) .
$${let}\:{put}\:\varphi\left({t}\right)=\:{ln}\left(\mathrm{1}+{x}\right)−\left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:\:{for}\:{x}\geqslant\mathrm{0}\:{we}\:{have} \\ $$$$\varphi^{'} \left({t}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:−\left(\mathrm{1}−{x}\right)=\frac{\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}}=\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}\:\geqslant\mathrm{0}\:{so}\:\varphi\:{is} \\ $$$${increasing}\:\:{on}\:\left[\mathrm{0},+\infty\left[\:{we}\:{have}\:\varphi\left(\mathrm{0}\right)=\mathrm{0}\:\geqslant\mathrm{0}\:\Rightarrow\:\forall\:{x}\geqslant\mathrm{0}\right.\right. \\ $$$$\varphi\left({x}\right)\geqslant\mathrm{0}\:\:{we}\:{use}\:{the}\:{same}\:{method}\:\:{for}\:{the}\:{function} \\ $$$$\psi\left({x}\right)=\:{x}−{ln}\left(\mathrm{1}+{x}\right)\:{and}\:{we}\:{show}\:{that}\:\psi\left({x}\right)\geqslant\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{ln}\left({u}_{{n}} \right)=\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\:\frac{{k}}{{n}^{\mathrm{2}} }\right)\:{but}\: \\ $$$$\frac{{k}}{{n}^{\mathrm{2}} }\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant{ln}\:\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:\leqslant\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{n}^{\mathrm{2}} }−\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }{n}\left({n}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\leqslant{ln}\left({u}_{{n}} \right)\leqslant\:\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }{n}\left({n}+\mathrm{1}\right)\Rightarrow \\ $$$$\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{12}{n}^{\mathrm{3}} }\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\:\leqslant{ln}\left({u}_{{n}} \right)\leqslant\:\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:\:{but} \\ $$$${lim}_{{n}\rightarrow\infty} \:\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{3}} }=\:\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{lim}_{{n}\rightarrow\infty} \frac{{n}+\mathrm{1}}{\mathrm{2}{n}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow\infty} {ln}\left({u}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{lim}_{{n}\rightarrow\infty} {u}_{{n}} =\:\sqrt{{e}}\:\:\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *