Menu Close

Prove-that-1-x-x-2-1-2x-3x-2-1-2-1-2-2-3x-3-4x-2-

Tinku Tara 0 Comments
Pin




Question Number 2795 by Rasheed Soomro last updated on 27/Nov/15
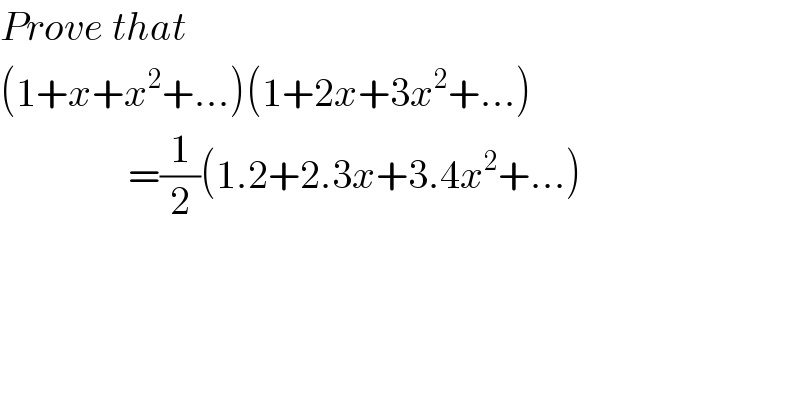
Prove that (1+x+x^2 +...)(1+2x+3x^2 +...) =(1/2)(1.2+2.3x+3.4x^2 +...)
$${Prove}\:{that} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{3}{x}+\mathrm{3}.\mathrm{4}{x}^{\mathrm{2}} +…\right) \\ $$
Answered by prakash jain last updated on 27/Nov/15
A=(1+x+x^2 +...) B=(1+2x+3x^2 +4x^3 ) Let us call coefficient of x^n in A=a_n =1 Let us call coefficient of x^n in B=b_n =(n+1) coefficient of x_n in product= a_0 b_n +a_1 b_(n−1) +a_2 b_(n−2) +...+a_n b_0 =(n+1)+(n)+(n−1)+...+1 =(((n+1)(n+2))/2) A∙B=Σ_(i=1) ^∞ (((i+1)(i+2))/2)x^i =(1/2)Σ_(i=1) ^∞ (i+1)(i+2)x^i =(1/2)(1∙2+2∙3x+3∙4x^2 +4∙5x^3 +...)
$${A}=\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right) \\ $$$${B}=\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} \right) \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{call}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{n}} \:{in}\:{A}={a}_{{n}} =\mathrm{1} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{call}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{n}} \:{in}\:{B}={b}_{{n}} =\left({n}+\mathrm{1}\right) \\ $$$${coefficient}\:{of}\:{x}_{{n}} \:{in}\:{product}= \\ $$$$\:\:\:\:{a}_{\mathrm{0}} {b}_{{n}} +{a}_{\mathrm{1}} {b}_{{n}−\mathrm{1}} +{a}_{\mathrm{2}} {b}_{{n}−\mathrm{2}} +…+{a}_{{n}} {b}_{\mathrm{0}} \\ $$$$\:\:\:=\left({n}+\mathrm{1}\right)+\left({n}\right)+\left({n}−\mathrm{1}\right)+…+\mathrm{1} \\ $$$$\:\:\:=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}} \\ $$$${A}\centerdot{B}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{1}\right)\left({i}+\mathrm{2}\right)}{\mathrm{2}}{x}^{{i}} =\frac{\mathrm{1}}{\mathrm{2}}\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\left({i}+\mathrm{1}\right)\left({i}+\mathrm{2}\right){x}^{{i}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\centerdot\mathrm{2}+\mathrm{2}\centerdot\mathrm{3}{x}+\mathrm{3}\centerdot\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}\centerdot\mathrm{5}{x}^{\mathrm{3}} +…\right) \\ $$
Answered by Yozzi last updated on 27/Nov/15
The Maclaurin series of (1/(1−x)) gives (1/(1−x))=1+x+x^2 +x^3 +...=Σ_(r=0) ^∞ x^r PROOF: Let f(x)=(1/(1−x)) ,x∈R−{1}. Differentiating we get f^((0)) (x)=(1−x)^(−1) f^((1)) (x)=(1−x)^(−2) f^((2)) (x)=2(1−x)^(−3) f^((3)) (x)=6(1−x)^(−4) . I conject that f^((n)) (x)=n!(1−x)^(−n−1) where f^((n)) (x) denotes the nth derivative of f(x)=(1−x)^(−1) (x≠1) and n∈N∪{0}. Let P(n) be the proposition that f^((n)) (x)=n!(1−x)^(−n−1) as conjectured. For n=0, P(0) gives f^((0)) =0!(1−x)^(−0−1) f^((0)) (x)=1×(1−x)^(−1) =(1−x)^(−1) which is f(x) differentiated zero times. Therefore, P(n) is true when n=0. Assume now that P(n) is true when n=k: f^((k)) (x)=k!(1−x)^(−k−1) . Fot n=k+1, f^((k+1)) (x)=(d/dx)(f^((k)) (x)) =(d/dx)(k!(1−x)^(−k−1) ) =(−k−1)(−1)k!(1−x)^(−k−2) =(k+1)k!(1−x)^(−k−2) f^((k+1)) (x)=(k+1)!(1−x)^(−(k+1)−1) So, P(k+1) is true, assuming P(k) is true. Since P(0) is true then,by the principle of mathematical induction, P(n) is true for all non−negative integers. Hence, f(x) is infinitely differentiable for x≠1 and f(x) with all its derivatives are defined at x=0. We can then obtain the Maclaurin series expansion of f(x)=(1/(1−x)). This is given by f(x)=Σ_(r=0) ^∞ ((x^r f^((r)) (0))/(r!)) Since f^((r)) (x)=r!(1−x)^(−r−1) f(x)=Σ_(r=0) ^∞ (x^r /(r!))×r!(1−0)^(−r−1) f(x)=Σ_(r=0) ^∞ x^r Therefore, (1/(1−x))=Σ_(r=0) ^∞ x^r . □ Observe that 1+2x+3x^2 +4x^3 +...=Σ_(r=1) ^∞ rx^(r−1) R.H.S=Σ_(r=1) ^∞ (d/dx)(x^r ). The series is term by term differentiable. ∴ Σ_(r=1) ^∞ (d/dx)(x^r )=(d/dx)(Σ_(r=1) ^∞ x^r )=(d/dx)(xΣ_(r=1) ^∞ x^(r−1) ). Now,Σ_(r=1) ^∞ x^(r−1) =Σ_(r=0) ^∞ x^r =(1/(1−x)). ∴R.H.S=(d/dx)((x/(1−x))) =(((1−x)×1−(−1)(x))/((1−x)^2 )) (Quotient rule) =((1−x+x)/((1−x)^2 )) R.H.S=(1/((1−x)^2 )). ∴ Σ_(r=1) ^∞ rx^(r−1) =(1/((1−x)^2 )). The L.H.S product of the equation in question becomes (Σ_(r=0) ^∞ x^r )(Σ_(r=1) ^∞ rx^(r−1) )=(1/(1−x))×(1/((1−x)^2 )) L.H.S=(1/((1−x)^3 )). Let g(x)=(1−x)^(−3) . g^((1)) (x)=3(1−x)^(−4) =((3!)/(2!))(1−x)^(−4) g^((2)) (x)=3×4(1−x)^(−5) =((4!)/(2!))(1−x)^(−5) g^((3)) (x)=3×4×5(1−x)^(−6) =((5!)/(2!))(1−x)^(−6) I thus state without proof that the nth derivative
$${The}\:{Maclaurin}\:{series}\:{of}\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{gives} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}=\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{r}} \\ $$$$ \\ $$$$\mathrm{PROOF}:\: \\ $$$${Let}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:,{x}\in\mathbb{R}−\left\{\mathrm{1}\right\}. \\ $$$${Differentiating}\:{we}\:{get} \\ $$$${f}^{\left(\mathrm{0}\right)} \left({x}\right)=\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} \\ $$$${f}^{\left(\mathrm{1}\right)} \left({x}\right)=\left(\mathrm{1}−{x}\right)^{−\mathrm{2}} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}\left(\mathrm{1}−{x}\right)^{−\mathrm{3}} \\ $$$${f}^{\left(\mathrm{3}\right)} \left({x}\right)=\mathrm{6}\left(\mathrm{1}−{x}\right)^{−\mathrm{4}} . \\ $$$${I}\:{conject}\:{that}\:{f}^{\left({n}\right)} \left({x}\right)={n}!\left(\mathrm{1}−{x}\right)^{−{n}−\mathrm{1}} \\ $$$${where}\:{f}^{\left({n}\right)} \left({x}\right)\:{denotes}\:{the}\:{nth}\:{derivative} \\ $$$${of}\:{f}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} \:\left({x}\neq\mathrm{1}\right)\:{and}\:{n}\in\mathbb{N}\cup\left\{\mathrm{0}\right\}. \\ $$$$ \\ $$$${Let}\:{P}\left({n}\right)\:{be}\:{the}\:{proposition}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{f}^{\left({n}\right)} \left({x}\right)={n}!\left(\mathrm{1}−{x}\right)^{−{n}−\mathrm{1}} \\ $$$${as}\:{conjectured}. \\ $$$${For}\:{n}=\mathrm{0},\:{P}\left(\mathrm{0}\right)\:{gives}\:{f}^{\left(\mathrm{0}\right)} =\mathrm{0}!\left(\mathrm{1}−{x}\right)^{−\mathrm{0}−\mathrm{1}} \\ $$$${f}^{\left(\mathrm{0}\right)} \left({x}\right)=\mathrm{1}×\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} =\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} \\ $$$${which}\:{is}\:{f}\left({x}\right)\:{differentiated}\:{zero}\:{times}. \\ $$$${Therefore},\:{P}\left({n}\right)\:{is}\:{true}\:{when}\:{n}=\mathrm{0}. \\ $$$${Assume}\:{now}\:{that}\:{P}\left({n}\right)\:{is}\:{true}\:{when} \\ $$$${n}={k}:\:\:{f}^{\left({k}\right)} \left({x}\right)={k}!\left(\mathrm{1}−{x}\right)^{−{k}−\mathrm{1}} . \\ $$$${Fot}\:{n}={k}+\mathrm{1}, \\ $$$${f}^{\left({k}+\mathrm{1}\right)} \left({x}\right)=\frac{{d}}{{dx}}\left({f}^{\left({k}\right)} \left({x}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{d}}{{dx}}\left({k}!\left(\mathrm{1}−{x}\right)^{−{k}−\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−{k}−\mathrm{1}\right)\left(−\mathrm{1}\right){k}!\left(\mathrm{1}−{x}\right)^{−{k}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({k}+\mathrm{1}\right){k}!\left(\mathrm{1}−{x}\right)^{−{k}−\mathrm{2}} \\ $$$${f}^{\left({k}+\mathrm{1}\right)} \left({x}\right)=\left({k}+\mathrm{1}\right)!\left(\mathrm{1}−{x}\right)^{−\left({k}+\mathrm{1}\right)−\mathrm{1}} \\ $$$${So},\:{P}\left({k}+\mathrm{1}\right)\:{is}\:{true},\:{assuming}\:{P}\left({k}\right)\:{is} \\ $$$${true}.\:{Since}\:{P}\left(\mathrm{0}\right)\:{is}\:{true}\:{then},{by}\:{the} \\ $$$${principle}\:{of}\:{mathematical}\:{induction}, \\ $$$${P}\left({n}\right)\:{is}\:{true}\:{for}\:{all}\:{non}−{negative}\: \\ $$$${integers}.\: \\ $$$$ \\ $$$${Hence},\:{f}\left({x}\right)\:{is}\:{infinitely}\:{differentiable} \\ $$$${for}\:{x}\neq\mathrm{1}\:{and}\:{f}\left({x}\right)\:{with}\:{all}\:{its}\:{derivatives}\:{are} \\ $$$${defined}\:{at}\:{x}=\mathrm{0}.\:{We}\:{can}\:{then}\:{obtain}\: \\ $$$${the}\:{Maclaurin}\:{series}\:{expansion}\:{of} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}.\:{This}\:{is}\:{given}\:{by} \\ $$$${f}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{r}} {f}^{\left({r}\right)} \left(\mathrm{0}\right)}{{r}!} \\ $$$${Since}\:{f}^{\left({r}\right)} \left({x}\right)={r}!\left(\mathrm{1}−{x}\right)^{−{r}−\mathrm{1}} \\ $$$${f}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{r}} }{{r}!}×{r}!\left(\mathrm{1}−\mathrm{0}\right)^{−{r}−\mathrm{1}} \\ $$$${f}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{r}} \\ $$$${Therefore},\:\frac{\mathrm{1}}{\mathrm{1}−{x}}=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{r}} .\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$$ \\ $$$${Observe}\:{that}\: \\ $$$$\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +…=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{rx}^{{r}−\mathrm{1}} \\ $$$${R}.{H}.{S}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{d}}{{dx}}\left({x}^{{r}} \right). \\ $$$${The}\:{series}\:{is}\:{term}\:{by}\:{term}\:{differentiable}. \\ $$$$\therefore\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{d}}{{dx}}\left({x}^{{r}} \right)=\frac{{d}}{{dx}}\left(\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{r}} \right)=\frac{{d}}{{dx}}\left({x}\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{r}−\mathrm{1}} \right). \\ $$$${Now},\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{r}−\mathrm{1}} =\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}. \\ $$$$\therefore{R}.{H}.{S}=\frac{{d}}{{dx}}\left(\frac{{x}}{\mathrm{1}−{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{1}−{x}\right)×\mathrm{1}−\left(−\mathrm{1}\right)\left({x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\:\left({Quotient}\:{rule}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}−{x}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${R}.{H}.{S}=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }.\:\therefore\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{rx}^{{r}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }. \\ $$$${The}\:{L}.{H}.{S}\:{product}\:{of}\:{the}\:{equation} \\ $$$${in}\:{question}\:{becomes} \\ $$$$\left(\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{r}} \right)\left(\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{rx}^{{r}−\mathrm{1}} \right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}×\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${L}.{H}.{S}=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }. \\ $$$${Let}\:{g}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{−\mathrm{3}} . \\ $$$${g}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{3}\left(\mathrm{1}−{x}\right)^{−\mathrm{4}} =\frac{\mathrm{3}!}{\mathrm{2}!}\left(\mathrm{1}−{x}\right)^{−\mathrm{4}} \\ $$$${g}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{3}×\mathrm{4}\left(\mathrm{1}−{x}\right)^{−\mathrm{5}} =\frac{\mathrm{4}!}{\mathrm{2}!}\left(\mathrm{1}−{x}\right)^{−\mathrm{5}} \\ $$$${g}^{\left(\mathrm{3}\right)} \left({x}\right)=\mathrm{3}×\mathrm{4}×\mathrm{5}\left(\mathrm{1}−{x}\right)^{−\mathrm{6}} =\frac{\mathrm{5}!}{\mathrm{2}!}\left(\mathrm{1}−{x}\right)^{−\mathrm{6}} \\ $$$${I}\:{thus}\:{state}\:{without}\:{proof}\:\:{that}\:{the}\:{nth}\:{derivative} \\ $$
Commented by Yozzi last updated on 27/Nov/15
I ran out of space...
$${I}\:{ran}\:{out}\:{of}\:{space}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *