Question Number 30206 by .none. last updated on 18/Feb/18
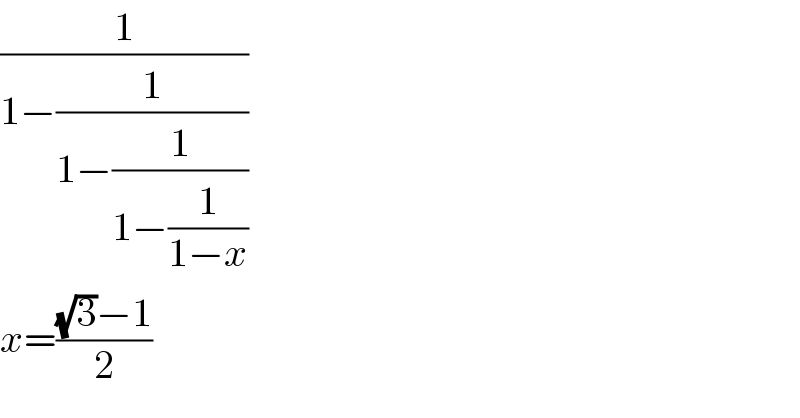
$$\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}}}} \\ $$$${x}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by abdo imad last updated on 18/Feb/18
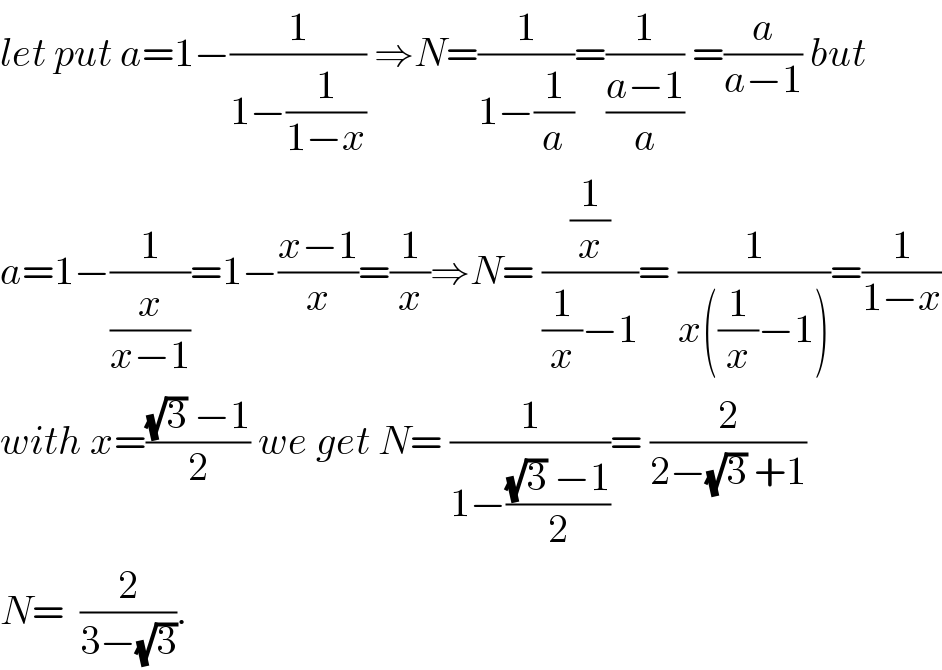
$${let}\:{put}\:{a}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}}\:\Rightarrow{N}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{a}}}=\frac{\mathrm{1}}{\frac{{a}−\mathrm{1}}{{a}}}\:=\frac{{a}}{{a}−\mathrm{1}}\:{but} \\ $$$${a}=\mathrm{1}−\frac{\mathrm{1}}{\frac{{x}}{{x}−\mathrm{1}}}=\mathrm{1}−\frac{{x}−\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{x}}\Rightarrow{N}=\:\frac{\frac{\mathrm{1}}{{x}}}{\frac{\mathrm{1}}{{x}}−\mathrm{1}}=\:\frac{\mathrm{1}}{{x}\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${with}\:{x}=\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{2}}\:{we}\:{get}\:{N}=\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{2}}}=\:\frac{\mathrm{2}}{\mathrm{2}−\sqrt{\mathrm{3}}\:+\mathrm{1}} \\ $$$${N}=\:\:\frac{\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{3}}}. \\ $$
Answered by ajfour last updated on 18/Feb/18
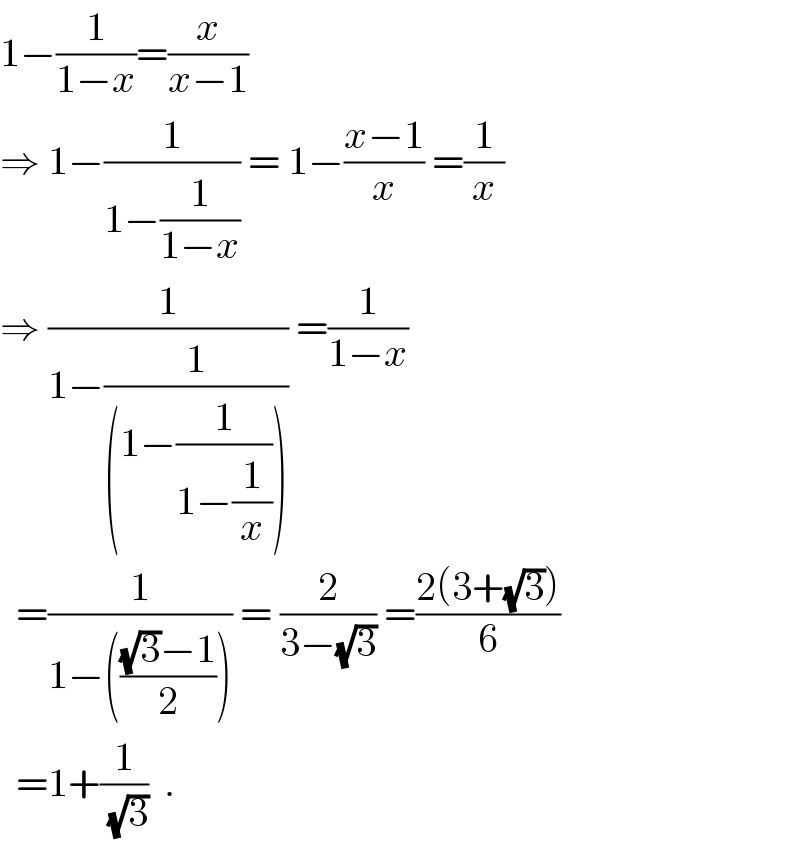
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}=\frac{{x}}{{x}−\mathrm{1}}\: \\ $$$$\Rightarrow\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}}\:=\:\mathrm{1}−\frac{{x}−\mathrm{1}}{{x}}\:=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{x}}}\right)}}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{3}}}\:=\frac{\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)}{\mathrm{6}} \\ $$$$\:\:=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\:. \\ $$
