Question Number 95742 by Abdulrahman last updated on 27/May/20
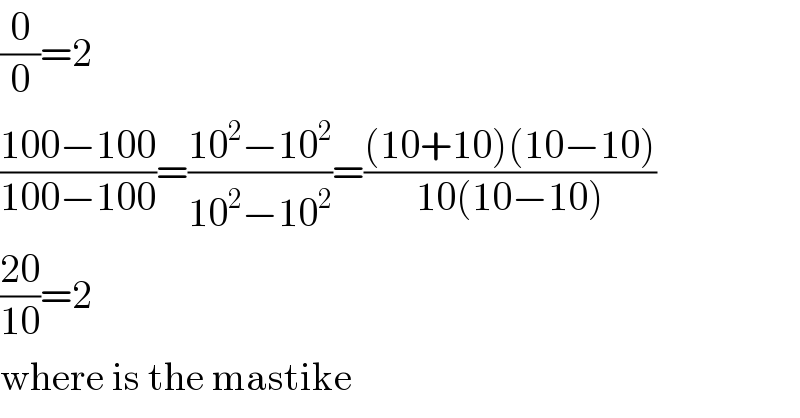
$$\frac{\mathrm{0}}{\mathrm{0}}=\mathrm{2} \\ $$$$\frac{\mathrm{100}−\mathrm{100}}{\mathrm{100}−\mathrm{100}}=\frac{\mathrm{10}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }{\mathrm{10}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }=\frac{\left(\mathrm{10}+\mathrm{10}\right)\left(\mathrm{10}−\mathrm{10}\right)}{\mathrm{10}\left(\mathrm{10}−\mathrm{10}\right)} \\ $$$$\frac{\mathrm{20}}{\mathrm{10}}=\mathrm{2} \\ $$$$\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mastike} \\ $$
Commented by bobhans last updated on 27/May/20
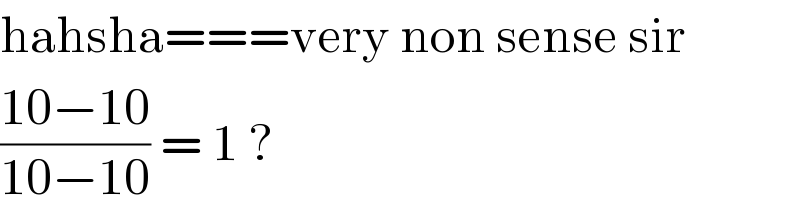
$$\mathrm{hahsha}===\mathrm{very}\:\mathrm{non}\:\mathrm{sense}\:\mathrm{sir}\: \\ $$$$\frac{\mathrm{10}−\mathrm{10}}{\mathrm{10}−\mathrm{10}}\:=\:\mathrm{1}\:? \\ $$
Commented by 200217 last updated on 27/May/20

$${We}\:{all}\:{know}\:{that}\:{it}'{s}\:{wrong}\:{but} \\ $$$${that}'{s}\:{the}\:{beauty}\:{if}\:{mathematical} \\ $$$${fallacy} \\ $$
Answered by mathmax by abdo last updated on 27/May/20
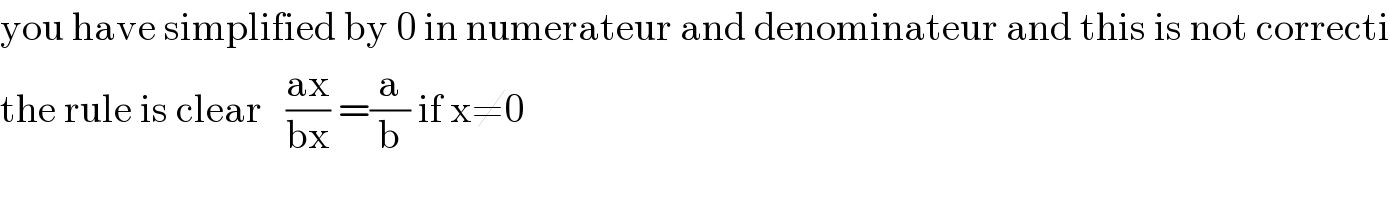
$$\mathrm{you}\:\mathrm{have}\:\mathrm{simplified}\:\mathrm{by}\:\mathrm{0}\:\mathrm{in}\:\mathrm{numerateur}\:\mathrm{and}\:\mathrm{denominateur}\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correcti} \\ $$$$\mathrm{the}\:\mathrm{rule}\:\mathrm{is}\:\mathrm{clear}\:\:\:\frac{\mathrm{ax}}{\mathrm{bx}}\:=\frac{\mathrm{a}}{\mathrm{b}}\:\mathrm{if}\:\mathrm{x}\neq\mathrm{0}\: \\ $$
Answered by Rio Michael last updated on 28/May/20

$$\mathrm{hahaha}\:\mathrm{great}\:\mathrm{job}\:\mathrm{but}\:\mathrm{from}\:\mathrm{your}\:\mathrm{very}\:\mathrm{first}\:\mathrm{statement} \\ $$$$\frac{\mathrm{0}}{\mathrm{0}\:}\:\neq\:\mathrm{2}\:,\:\mathrm{so}\:\mathrm{thats}\:\mathrm{the}\:\mathrm{mistake} \\ $$$$\mathrm{without}\:\mathrm{that}\:\mathrm{everything}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{but}\:\mathrm{logically} \\ $$$$\mathrm{it}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{make}\:\mathrm{sense}. \\ $$
