Question Number 68349 by peter frank last updated on 09/Sep/19

Answered by mr W last updated on 09/Sep/19
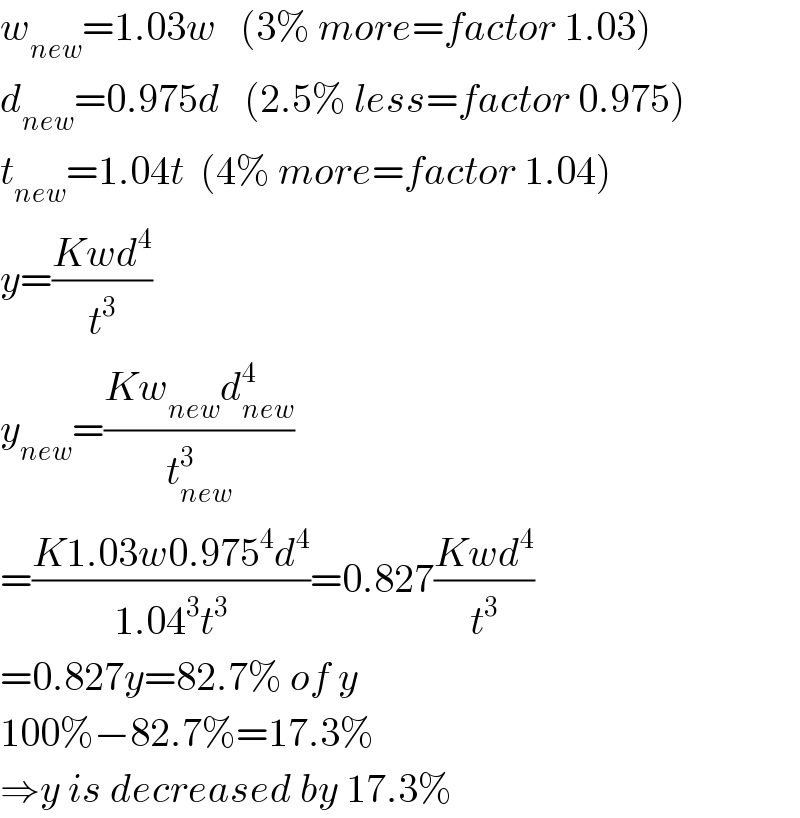
$${w}_{{new}} =\mathrm{1}.\mathrm{03}{w}\:\:\:\left(\mathrm{3\%}\:{more}={factor}\:\mathrm{1}.\mathrm{03}\right) \\ $$$${d}_{{new}} =\mathrm{0}.\mathrm{975}{d}\:\:\:\left(\mathrm{2}.\mathrm{5\%}\:{less}={factor}\:\mathrm{0}.\mathrm{975}\right) \\ $$$${t}_{{new}} =\mathrm{1}.\mathrm{04}{t}\:\:\left(\mathrm{4\%}\:{more}={factor}\:\mathrm{1}.\mathrm{04}\right) \\ $$$${y}=\frac{{Kwd}^{\mathrm{4}} }{{t}^{\mathrm{3}} } \\ $$$${y}_{{new}} =\frac{{Kw}_{{new}} {d}_{{new}} ^{\mathrm{4}} }{{t}_{{new}} ^{\mathrm{3}} } \\ $$$$=\frac{{K}\mathrm{1}.\mathrm{03}{w}\mathrm{0}.\mathrm{975}^{\mathrm{4}} {d}^{\mathrm{4}} }{\mathrm{1}.\mathrm{04}^{\mathrm{3}} {t}^{\mathrm{3}} }=\mathrm{0}.\mathrm{827}\frac{{Kwd}^{\mathrm{4}} }{{t}^{\mathrm{3}} } \\ $$$$=\mathrm{0}.\mathrm{827}{y}=\mathrm{82}.\mathrm{7\%}\:{of}\:{y} \\ $$$$\mathrm{100\%}−\mathrm{82}.\mathrm{7\%}=\mathrm{17}.\mathrm{3\%} \\ $$$$\Rightarrow{y}\:{is}\:{decreased}\:{by}\:\mathrm{17}.\mathrm{3\%} \\ $$
Commented by peter frank last updated on 09/Sep/19
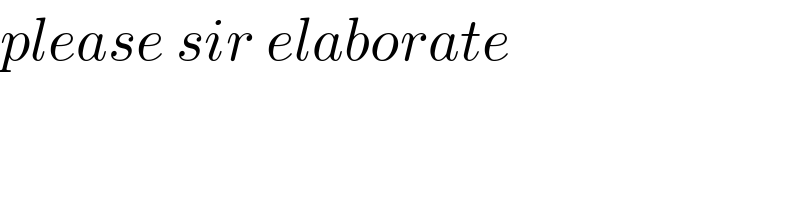
$${please}\:{sir}\:{elaborate} \\ $$
Commented by peter frank last updated on 21/Sep/19

$${thank}\:{you} \\ $$
