Question Number 30366 by diyatrivedi last updated on 21/Feb/18
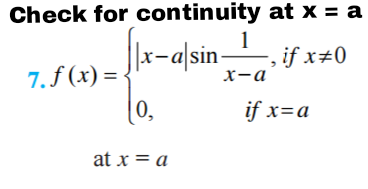
Commented by abdo imad last updated on 21/Feb/18
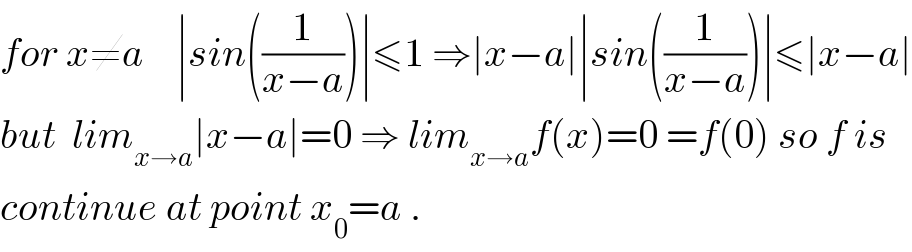
$${for}\:{x}\neq{a}\:\:\:\:\mid{sin}\left(\frac{\mathrm{1}}{{x}−{a}}\right)\mid\leqslant\mathrm{1}\:\Rightarrow\mid{x}−{a}\mid\mid{sin}\left(\frac{\mathrm{1}}{{x}−{a}}\right)\mid\leqslant\mid{x}−{a}\mid \\ $$$${but}\:\:{lim}_{{x}\rightarrow{a}} \mid{x}−{a}\mid=\mathrm{0}\:\Rightarrow\:{lim}_{{x}\rightarrow{a}} {f}\left({x}\right)=\mathrm{0}\:={f}\left(\mathrm{0}\right)\:{so}\:{f}\:{is} \\ $$$${continue}\:{at}\:{point}\:{x}_{\mathrm{0}} ={a}\:. \\ $$
